1.(2025·南通期末)下列各式计算结果为负数的是().
A.$3+(-2)$
B.$3-(-2)$
C.$3×(-2)$
D.$(-3)^2$

2.(2025·南通启东期末)下列结果最小的是().
A.$-3-\frac{1}{2}$
B.$-3+\frac{1}{2}$
C.$-3×(-\frac{1}{2})$
D.$-3÷(-\frac{1}{2})$

3.(2024·甘肃白银期末)对于有理数$a,b$,定义一种新运算,规定$a☆b= a^2-|b|$,则$2☆(-3)= $.

4. 教材 P60例4·变式 计算：
(1)$-2^4+(3-7)^2-2$；
(2)$(\frac{1}{2}+\frac{5}{6}-\frac{7}{12})÷(-\frac{1}{6})^2$.

5. 中考新考法 新定义问题 定义：一种对于三位数$\overline{abc}$(其中$a$在百位,$b$在十位,$c$在个位,$a,b,c$不完全相同)的“F运算”：重排$\overline{abc}$的三个数位上的数字,计算所得最大三位数和最小三位数的差(允许百位数字为零),例如$\overline{abc}= 463$时,则$463\xrightarrow{F运算}297$($643 - 346= 297$)$\xrightarrow{F运算}693$($972 - 279= 693$)经过大量运算,我们发现任意一个三位数经过若干次“F运算”都会得到一个固定不变的值；类比联想到：任意一个四位数经过若干次这样的“F运算”也会得到一个定值,这个定值为().
A.4159
B.6419
C.5179
D.6174

6.(2025·扬州邗江区期末)已知$a,b$互为相反数,$c,d$互为倒数,且$|m|= 5$,则$\frac{a+b}{2025}+(-cd)^{2025}+m^2$的值为.

7.(1)在玩“24点”游戏时,“3,3,7,7”列式并计算为$7×(3+\frac{3}{7})= 7×3 + 3= 24$是依据运算律：；
(2)如图,小明抽到以下4张牌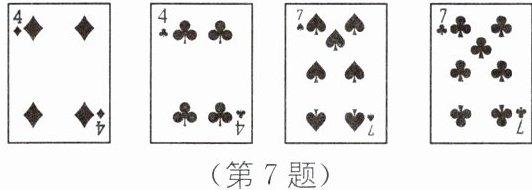：请你帮他写出运算结果为24的一个算式：；
(3)如果红桃、方片表示正,黑桃、梅花表示负,请你用(2)中的4张牌表示的数写出运算结果为24的一个算式：.