1. 如图,用火柴棍拼成一排由三角形组成的图形,如果图形中含有2,3或4个三角形,分别需要多少根火柴棍?如果图形中含有n个三角形,需要多少根火柴棍?
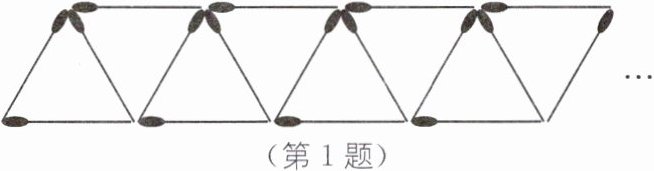

答案:当图形中含有2,3或4个三角形时,分别需要5,7,9根火柴棍;第n个图形需要(2n+1)个.
解析:
当图形中含有2个三角形时,需要5根火柴棍;含有3个三角形时,需要7根火柴棍;含有4个三角形时,需要9根火柴棍;含有n个三角形时,需要$2n + 1$根火柴棍。
变式1.1 (2025·四川成都期末)如图是一组有规律的图案,第1个图案由3个基础图形组成,第2个图案由5个基础图形组成,…,则第n(n是正整数)个图案由
(1+2n)
个基础图形组成.答案:(1+2n)
变式1.2 跨学科 分子结构模型 (2025·济宁金乡一模改编)烷烃是一类由碳、氢元素组成的有机化合物,如图是这类物质前四种化合物的分子结构模型图,其中灰球代表碳原子,白球代表氢原子. 第1种(如图(1))有4个氢原子,第2种(如图(2))有6个氢原子,第3种(如图(3))有8个氢原子,…,按照这一规律,第15种化合物的分子结构模型中氢原子的个数是______

32
.
答案:32
解析:
第1种有4个氢原子,第2种有6个氢原子,第3种有8个氢原子,观察可知氢原子个数依次增加2。
设第n种化合物的氢原子个数为$a_n$,则$a_1 = 4$,$a_2 = 6$,$a_3 = 8$,公差$d = 2$。
等差数列通项公式为$a_n = a_1 + (n - 1)d$,代入得$a_n = 4 + (n - 1)×2 = 2n + 2$。
当$n = 15$时,$a_{15} = 2×15 + 2 = 32$。
32
设第n种化合物的氢原子个数为$a_n$,则$a_1 = 4$,$a_2 = 6$,$a_3 = 8$,公差$d = 2$。
等差数列通项公式为$a_n = a_1 + (n - 1)d$,代入得$a_n = 4 + (n - 1)×2 = 2n + 2$。
当$n = 15$时,$a_{15} = 2×15 + 2 = 32$。
32
变式1.3 (2025·上海青浦区期末)探索规律,并回答问题:观察如图各图形,我们会发现:图(1)空白部分小正方形的个数是$2^2 - 1^2 = 2 + 1$;图(2)空白部分小正方形的个数是$3^2 - 2^2 = 3 + 2$;图(3)空白部分小正方形的个数是$4^2 - 3^2 = 4 + 3$;像这样继续排列下去,可以用含有字母n的代数式表示为:
(n+1)²-n²=n+n+1
.(其中n为正整数)答案:(n+1)²-n²=n+n+1
解析:
$(n+1)^2 - n^2 = n + (n + 1)$
变式1.4 方程思想 (2025·河北唐山遵化期末)围棋起源于中国,是一种策略型两人棋类游戏,中国古时称“弈”,春秋战国时期即有记载. 老师带领学生以围棋为道具摆出如图四幅图.

[观察思考]
第1个图形有10颗棋子,第2个图形一共有16颗棋子,第3个图形一共有22颗棋子,第4个图形一共有28颗棋子,…,以此类推.
[规律总结]
(1)第n个图形中棋子的颗数为______(用含n的代数式表示);
[问题解决]
(2)若按上面的规律摆出的一个图形有184颗棋子,则这是第______个图形.
[答案]:(1)
(2)

[观察思考]
第1个图形有10颗棋子,第2个图形一共有16颗棋子,第3个图形一共有22颗棋子,第4个图形一共有28颗棋子,…,以此类推.
[规律总结]
(1)第n个图形中棋子的颗数为______(用含n的代数式表示);
[问题解决]
(2)若按上面的规律摆出的一个图形有184颗棋子,则这是第______个图形.
[答案]:(1)
6n+4
;(2)
30
答案:
(1)6n+4;
(2)30
(1)6n+4;
(2)30
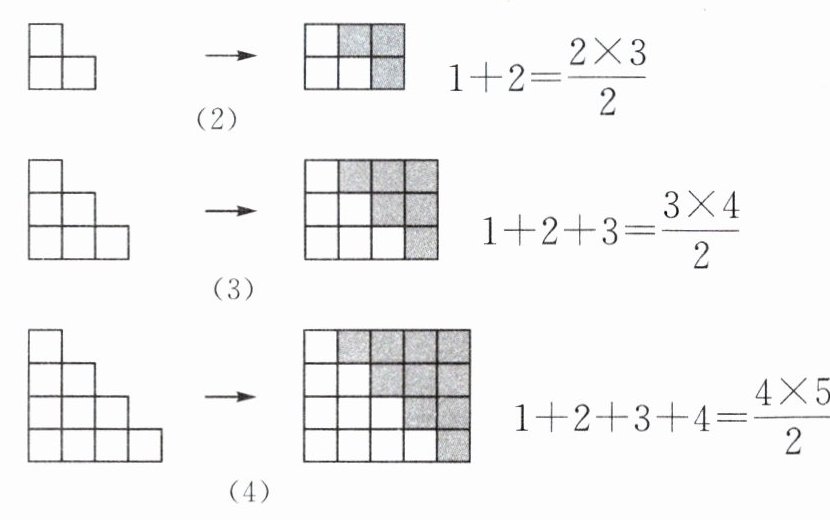
变式1.5 (2025·徐州期中)如图,每个图形都由同样大小的小正方形按照一定的规律组成,每个小正方形的面积是1. 根据图形与等式的关系解答下列问题:

(1)直接写出图(10)所反映的算式;
(2)猜想并直接写出图(n)所反映的算式;
(3)根据(2)的结论计算:1001+1002+1003+…+2023+2024.

(1)直接写出图(10)所反映的算式;

(2)猜想并直接写出图(n)所反映的算式;
(3)根据(2)的结论计算:1001+1002+1003+…+2023+2024.
答案:
(1)1+2+3+4+…+9+10=10×11/2;
(2)1+2+3+4+…+n=n(n+1)/2;
(3)1548800
(1)1+2+3+4+…+9+10=10×11/2;
(2)1+2+3+4+…+n=n(n+1)/2;
(3)1548800