10. 假设●,▲,■表示三种不同的物体,现用天平称了两次,情况如图所示,那么▲和■,●和▲两种物体的质量之间有什么相等关系呢?
(1)用含有符号●,▲,■的等式加以表示;
(2)使用字母表示(1)中的相等关系,并使字母的系数为尽量小的整数.

(1)用含有符号●,▲,■的等式加以表示;
(2)使用字母表示(1)中的相等关系,并使字母的系数为尽量小的整数.

答案:
(1)3▲=2■,3●=▲+●.
(2)设物体▲的质量为x,物体■的质量为y,则3x=2y.设物体●的质量为z,则3z=x+z,即2z=x.
(1)3▲=2■,3●=▲+●.
(2)设物体▲的质量为x,物体■的质量为y,则3x=2y.设物体●的质量为z,则3z=x+z,即2z=x.
11.(2024·广东佛山南海区期末)综合与实践 某兴趣小组利用长为$a$厘米,宽为$b$厘米的长方形纸板制作长方体纸盒,做了以下尝试:(纸板厚度及接缝处忽略不计)
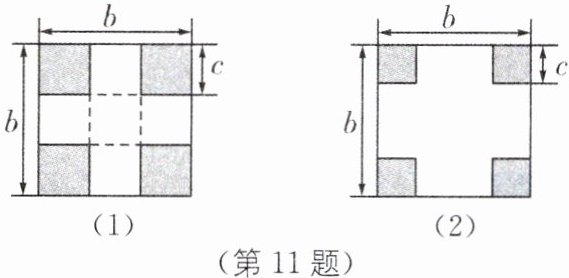
(1)如图(1),若$a= b$,先在纸板四角剪去4个同样大小边长为$c$厘米的小正方形,再沿虚线折起来就可以做成一个无盖的正方体纸盒,此时$b与c$的数量关系为______
(2)如图(2),若$a= b$,先在纸板四角剪去4个同样大小边长为$c$厘米的小正方形,再沿虚线折起来就可以做成一个无盖的长方体纸盒,为了使纸盒底面更加牢固且达到废物利用的目的,将剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满,此时$b与c$的数量关系为______
(3)若$a= 20$,$b= 12$,在纸板四角剪去4个同样大小边长为$c$厘米的小正方形,恰好可以制作成一个无盖的长方体纸盒,请你通过列表研究,当$c$取何整数时,所得长方体的体积$V$最大?

| c/cm | 1 | 2 | 3 | 4 | 5 |
| V/cm^3 | 180 | 256 | 252 | 192 | 100 |

(1)如图(1),若$a= b$,先在纸板四角剪去4个同样大小边长为$c$厘米的小正方形,再沿虚线折起来就可以做成一个无盖的正方体纸盒,此时$b与c$的数量关系为______
b=3c
.(2)如图(2),若$a= b$,先在纸板四角剪去4个同样大小边长为$c$厘米的小正方形,再沿虚线折起来就可以做成一个无盖的长方体纸盒,为了使纸盒底面更加牢固且达到废物利用的目的,将剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满,此时$b与c$的数量关系为______
b=4c
.(3)若$a= 20$,$b= 12$,在纸板四角剪去4个同样大小边长为$c$厘米的小正方形,恰好可以制作成一个无盖的长方体纸盒,请你通过列表研究,当$c$取何整数时,所得长方体的体积$V$最大?

| c/cm | 1 | 2 | 3 | 4 | 5 |
| V/cm^3 | 180 | 256 | 252 | 192 | 100 |
由表格中的数据,可知当c≥2时,随着c的增大,体积V逐渐减小,并且当c=2时,V的值大于c=1时V的值,∴当c=2时,所得长方体的体积V最大。
答案:
(1)b=3c [解析]由题意,得b-2c=c,
∴b=3c.
(2)b=4c [解析]
∵在纸板四角剪去四个同样大小边长为c厘米的小正方形,
∴剩余长为b-2c.
∵剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满,
∴此时的长为2c,
∴b-2c=2c,
∴b=4c.
(3)由表格中的数据,可知当c≥2时,随着c的增大,体积V逐渐减小,并且当c=2时,V的值大于c=1时V的值,
∴当c=2时,所得长方体的体积V最大.
(1)b=3c [解析]由题意,得b-2c=c,
∴b=3c.
(2)b=4c [解析]
∵在纸板四角剪去四个同样大小边长为c厘米的小正方形,
∴剩余长为b-2c.
∵剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满,
∴此时的长为2c,
∴b-2c=2c,
∴b=4c.
(3)由表格中的数据,可知当c≥2时,随着c的增大,体积V逐渐减小,并且当c=2时,V的值大于c=1时V的值,
∴当c=2时,所得长方体的体积V最大.