4. 教材P130习题T14·变式(2025·扬州期末)现有一种新型网约车是一种全无人驾驶的网约车,已经在全国多个城市开放运营.某城市的新型网约车的计价规则如表:
| 计费项目 | 里程费 | 时长费 | 远途费 |
| 单价 | 2元/千米 | 0.5元/分钟 | 1元/千米 |

(注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算,时长费按行车的实际时间计算,远途费的收取方式为:行车里程15千米以内(含15千米)不收远途费,超过15千米的,超出部分每千米加收1元)
(1)若小东乘坐新型网约车,行车里程为20千米,行车时间为20分钟,则需付车费
(2)若小明两次乘坐新型网约车,第一次行车里程为18千米,第二次行车里程为8千米,发现第一次行车时间是第二次的两倍且所付车费比第二次多28.5元,则小明第一次乘坐网约车的行车时间为
(3)小王和小张各自乘坐新型网约车,小王比小张的行车里程少3千米,行程结束后反而多付了6元,两人计费项目也相同(远途费为0时视为没有这个计费项目),那么这两辆新型网约车的行车时长相差______分钟.(直接写出答案)
| 计费项目 | 里程费 | 时长费 | 远途费 |
| 单价 | 2元/千米 | 0.5元/分钟 | 1元/千米 |

(注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算,时长费按行车的实际时间计算,远途费的收取方式为:行车里程15千米以内(含15千米)不收远途费,超过15千米的,超出部分每千米加收1元)
(1)若小东乘坐新型网约车,行车里程为20千米,行车时间为20分钟,则需付车费
55
元?(2)若小明两次乘坐新型网约车,第一次行车里程为18千米,第二次行车里程为8千米,发现第一次行车时间是第二次的两倍且所付车费比第二次多28.5元,则小明第一次乘坐网约车的行车时间为
22
分钟?(3)小王和小张各自乘坐新型网约车,小王比小张的行车里程少3千米,行程结束后反而多付了6元,两人计费项目也相同(远途费为0时视为没有这个计费项目),那么这两辆新型网约车的行车时长相差______分钟.(直接写出答案)
24 或 30
答案:4.
(1)根据题意,得2×20+0.5×20+1×(20-15)=55(元).故需付车费 55 元.
(2)设小明第二次乘坐网约车的行车时间为 x 分钟,则小明第一次乘坐网约车的行车时间为 2x 分钟,根据题意,得2×18+0.5×2x+1×(18-15)-(2×8+0.5x)=28.5,解得x=11,
∴2x=2×11=22.故小明第一次乘坐网约车的行车时间为 22 分钟.
(3)24 或 30 [解析]设这两辆新型网约车的行车时长相差 y 分钟,当都没有远途费时,0.5y-2×3=6,解得x=24;当都有远途费时,0.5y-(2+1)×3=6,解得x=30.
∴这两辆新型网约车的行车时长相差 24 或 30 分钟.
(1)根据题意,得2×20+0.5×20+1×(20-15)=55(元).故需付车费 55 元.
(2)设小明第二次乘坐网约车的行车时间为 x 分钟,则小明第一次乘坐网约车的行车时间为 2x 分钟,根据题意,得2×18+0.5×2x+1×(18-15)-(2×8+0.5x)=28.5,解得x=11,
∴2x=2×11=22.故小明第一次乘坐网约车的行车时间为 22 分钟.
(3)24 或 30 [解析]设这两辆新型网约车的行车时长相差 y 分钟,当都没有远途费时,0.5y-2×3=6,解得x=24;当都有远途费时,0.5y-(2+1)×3=6,解得x=30.
∴这两辆新型网约车的行车时长相差 24 或 30 分钟.
5. (2025·广东惠州期末)某地天然气收费方案如下:
| 阶梯 | 年用气量 | 价格 | 补充说明 |
| 第一阶梯 |$ 0~400 m^3($含400)的部分 | 3元$/m^3 $| 当家庭人口超过3人时,每增加1人,第一、二阶梯年用气量上限将分别增加$100 m^3,150 m^3,$同时,第二、三阶梯年用气量下限随之调整,每一阶梯的价格保持不变 |
| 第二阶梯 |$ 400~800 m^3($含800)的部分 | 4元$/m^3 $| |
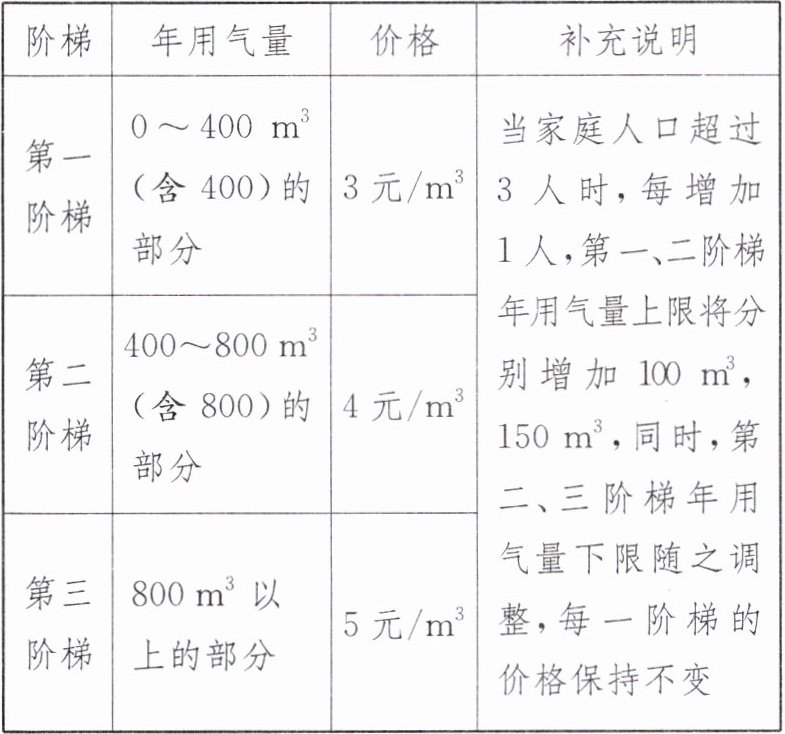
| 第三阶梯 |$ 800 m^3$以上的部分 | 5元$/m^3 $| |
(1)某家庭当年用气量为$500 m^3.$若该家庭人口为3人,则需缴纳天然气费用______元;若该家庭人口为4人,则需缴纳天然气费用______元.
(2)甲户家庭人口为3人,乙户家庭人口为4人.某年甲、乙两户年用气量之和为$1 000 m^3,$甲户年用气量大于乙户年用气量.已知甲、乙两户一共缴纳天然气费用3 200元,求甲、乙两户年用气量分别是多少.
(3)某公司共有22名员工,员工宿舍有3人间和4人间两种类型的房间可供选择,且员工所选择的房间必须住满.结算天然气费用时,将每间宿舍视作一户家庭,收费标准按上表进行收费.假定每位员工的年用气量为$250 m^3,$要使该公司员工宿舍当年总天然气费最低,则3人间的房间数为______间.
[答案]:5.
(1)
∵某家庭当年用气量为500m³,家庭人口为 3 人,
∴需缴纳天然气费用为3×400+4×(500-400)=1600(元).
∵该家庭当年用气量为500m³,家庭人口为 4 人,
∴需缴纳天然气费用为3×500=1500(元).
(2)设甲用户的年用气量为x m³,则乙用户的年用气量为(1000-x)m³.
∵甲户年用气量大于乙户年用气量,
∴x>500,
∴1000-x<500,
∴3×400+4×(x-400)+3×(1000-x)=3200.解得x=600.
∴1000-x=400.故甲、乙两户年用气量分别是600m³,400m³.
(3)
∵(22-3a)/4为正整数,
∴a=2 或 a=6,
∴4 人间有 4 间或 1 间.3 人间燃气用量为3×250=750(m³),4 人间燃气用量为4×250=1000(m³).①当 3 人间 2 间,4 人间 4 间时.需缴纳的天然气费用:2×[3×400+4×(750-400)]+4[3×500+4×(950-500)+5×(1000-950)]=19400(元).②当 3 人间 6 间,4 人间 1 间时.需缴纳的天然气费用:6×[3×400+4×(750-400)]+[3×500+4×(950-500)+5×(1000-950)]=19150(元).
∵19400>19150,
∴要使该公司员工宿舍当年总天然气费最低,则 3 人间的房间数为 6 间.
| 阶梯 | 年用气量 | 价格 | 补充说明 |
| 第一阶梯 |$ 0~400 m^3($含400)的部分 | 3元$/m^3 $| 当家庭人口超过3人时,每增加1人,第一、二阶梯年用气量上限将分别增加$100 m^3,150 m^3,$同时,第二、三阶梯年用气量下限随之调整,每一阶梯的价格保持不变 |
| 第二阶梯 |$ 400~800 m^3($含800)的部分 | 4元$/m^3 $| |

| 第三阶梯 |$ 800 m^3$以上的部分 | 5元$/m^3 $| |
(1)某家庭当年用气量为$500 m^3.$若该家庭人口为3人,则需缴纳天然气费用______元;若该家庭人口为4人,则需缴纳天然气费用______元.
(2)甲户家庭人口为3人,乙户家庭人口为4人.某年甲、乙两户年用气量之和为$1 000 m^3,$甲户年用气量大于乙户年用气量.已知甲、乙两户一共缴纳天然气费用3 200元,求甲、乙两户年用气量分别是多少.
(3)某公司共有22名员工,员工宿舍有3人间和4人间两种类型的房间可供选择,且员工所选择的房间必须住满.结算天然气费用时,将每间宿舍视作一户家庭,收费标准按上表进行收费.假定每位员工的年用气量为$250 m^3,$要使该公司员工宿舍当年总天然气费最低,则3人间的房间数为______间.
[答案]:5.
(1)
1600
1500
[解析]∵某家庭当年用气量为500m³,家庭人口为 3 人,
∴需缴纳天然气费用为3×400+4×(500-400)=1600(元).
∵该家庭当年用气量为500m³,家庭人口为 4 人,
∴需缴纳天然气费用为3×500=1500(元).
(2)设甲用户的年用气量为x m³,则乙用户的年用气量为(1000-x)m³.
∵甲户年用气量大于乙户年用气量,
∴x>500,
∴1000-x<500,
∴3×400+4×(x-400)+3×(1000-x)=3200.解得x=600.
∴1000-x=400.故甲、乙两户年用气量分别是600m³,400m³.
(3)
6
[解析]设 3 人间有 a 间,则 4 人间有(22-3a)/4间.∵(22-3a)/4为正整数,
∴a=2 或 a=6,
∴4 人间有 4 间或 1 间.3 人间燃气用量为3×250=750(m³),4 人间燃气用量为4×250=1000(m³).①当 3 人间 2 间,4 人间 4 间时.需缴纳的天然气费用:2×[3×400+4×(750-400)]+4[3×500+4×(950-500)+5×(1000-950)]=19400(元).②当 3 人间 6 间,4 人间 1 间时.需缴纳的天然气费用:6×[3×400+4×(750-400)]+[3×500+4×(950-500)+5×(1000-950)]=19150(元).
∵19400>19150,
∴要使该公司员工宿舍当年总天然气费最低,则 3 人间的房间数为 6 间.
答案:5.
(1)1600 1500 [解析]
∵某家庭当年用气量为500m³,家庭人口为 3 人,
∴需缴纳天然气费用为3×400+4×(500-400)=1600(元).
∵该家庭当年用气量为500m³,家庭人口为 4 人,
∴需缴纳天然气费用为3×500=1500(元).
(2)设甲用户的年用气量为x m³,则乙用户的年用气量为(1000-x)m³.
∵甲户年用气量大于乙户年用气量,
∴x>500,
∴1000-x<500,
∴3×400+4×(x-400)+3×(1000-x)=3200.解得x=600.
∴1000-x=400.故甲、乙两户年用气量分别是600m³,400m³.
(3)6 [解析]设 3 人间有 a 间,则 4 人间有(22-3a)/4间.
∵(22-3a)/4为正整数,
∴a=2 或 a=6,
∴4 人间有 4 间或 1 间.3 人间燃气用量为3×250=750(m³),4 人间燃气用量为4×250=1000(m³).①当 3 人间 2 间,4 人间 4 间时.需缴纳的天然气费用:2×[3×400+4×(750-400)]+4[3×500+4×(950-500)+5×(1000-950)]=19400(元).②当 3 人间 6 间,4 人间 1 间时.需缴纳的天然气费用:6×[3×400+4×(750-400)]+[3×500+4×(950-500)+5×(1000-950)]=19150(元).
∵19400>19150,
∴要使该公司员工宿舍当年总天然气费最低,则 3 人间的房间数为 6 间.
(1)1600 1500 [解析]
∵某家庭当年用气量为500m³,家庭人口为 3 人,
∴需缴纳天然气费用为3×400+4×(500-400)=1600(元).
∵该家庭当年用气量为500m³,家庭人口为 4 人,
∴需缴纳天然气费用为3×500=1500(元).
(2)设甲用户的年用气量为x m³,则乙用户的年用气量为(1000-x)m³.
∵甲户年用气量大于乙户年用气量,
∴x>500,
∴1000-x<500,
∴3×400+4×(x-400)+3×(1000-x)=3200.解得x=600.
∴1000-x=400.故甲、乙两户年用气量分别是600m³,400m³.
(3)6 [解析]设 3 人间有 a 间,则 4 人间有(22-3a)/4间.
∵(22-3a)/4为正整数,
∴a=2 或 a=6,
∴4 人间有 4 间或 1 间.3 人间燃气用量为3×250=750(m³),4 人间燃气用量为4×250=1000(m³).①当 3 人间 2 间,4 人间 4 间时.需缴纳的天然气费用:2×[3×400+4×(750-400)]+4[3×500+4×(950-500)+5×(1000-950)]=19400(元).②当 3 人间 6 间,4 人间 1 间时.需缴纳的天然气费用:6×[3×400+4×(750-400)]+[3×500+4×(950-500)+5×(1000-950)]=19150(元).
∵19400>19150,
∴要使该公司员工宿舍当年总天然气费最低,则 3 人间的房间数为 6 间.