1. (教材 P6 练习 T1·变式)(2025·福建厦门思明区期末)下面各组线段中,能组成三角形的是(
A.5,11,6
B.8,8,16
C.10,5,4
D.6,9,14
D
).A.5,11,6
B.8,8,16
C.10,5,4
D.6,9,14
答案:D [解析]A.
∵5+6=11,
∴不能组成三角形.故A选项错误;
B.
∵8+8=16,
∴不能组成三角形.故B选项错误;
C.
∵5+4<10,
∴不能组成三角形.故C选项错误;
D.
∵6+9>14,
∴能组成三角形.故D选项正确.故选D.
→只需要考虑两条较短的线段长度之和是否大于第三条线段的长度即可判定这三条线段能否构成一个三角形
∵5+6=11,
∴不能组成三角形.故A选项错误;
B.
∵8+8=16,
∴不能组成三角形.故B选项错误;
C.
∵5+4<10,
∴不能组成三角形.故C选项错误;
D.
∵6+9>14,
∴能组成三角形.故D选项正确.故选D.
→只需要考虑两条较短的线段长度之和是否大于第三条线段的长度即可判定这三条线段能否构成一个三角形
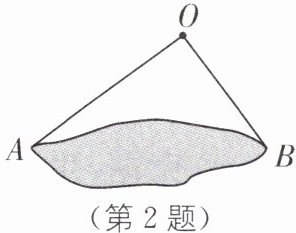
2. (2025·南通启东期中)如图,为估计池塘两岸 A,B 间的距离,小明在池塘一侧选取了一点 O,测得 OA= 16 m,OB= 12 m,那么 AB 的距离不可能是(
A.5 m
B.15 m
C.20 m
D.30 m
]
D
).
A.5 m
B.15 m
C.20 m
D.30 m
]
答案:D [解析]根据三角形的三边关系可得16-12<AB<16+12,即4<AB<28,
∴30 m不可能.故选D.
∴30 m不可能.故选D.
3. (2024·淮安中考)用一根小木棒与两根长度分别为 3 cm,5 cm 的小木棒组成三角形,则这根小木棒的长度可以是(
A.9 cm
B.7 cm
C.2 cm
D.1 cm
B
).A.9 cm
B.7 cm
C.2 cm
D.1 cm
答案:B [解析]设第三根木棒长为x cm,由三角形三边关系定理得5-3<x<5+3,所以x的取值范围是2<x<8,观察选项,只有选项B符合题意.故选B.
归纳总结 设三角形的两边长为a,b(a>b),则第三边长x的取值范围为a-b<x<a+b.
归纳总结 设三角形的两边长为a,b(a>b),则第三边长x的取值范围为a-b<x<a+b.
4. (2025·北京平谷区期中)若三角形的三边长分别为 3,4,x,则 x 的取值范围是(
A.3<x<4
B.1<x<7
C.0<x<7
D.2<x<6
B
).A.3<x<4
B.1<x<7
C.0<x<7
D.2<x<6
答案:B [解析]由题意,得4-3<x<4+3,即1<x<7.故选B.
5. (2024·扬州广陵区期末)如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为 3,4,5,7,且相邻两木条的夹角均可调整,若调整木条的夹角时不破坏此木框,则任两螺丝的距离的最大值是(

A.7
B.8
C.9
D.10
]
C
).
A.7
B.8
C.9
D.10
]
答案:C [解析]已知4条木条的长分别为3,4,5,7.
①选3+4,5,7作为三角形,则三边长为7,5,7.7-5<7<7+5,能构成三角形,此时两个螺丝间的最长距离为7;
②选4+5,3,7作为三角形,则三边长为9,3,7.7-3<9<7+3,能构成三角形,此时两个螺丝间的最大距离为9;
③选3+7,4,5作为三角形,则三边长为10,4,5.4+5<10,不能构成三角形,此种情况不成立;
④选5+7,3,4作为三角形,则三边长为12,3,4.而3+4<12,不能构成三角形,此种情况不成立.
综上所述,任两螺丝的距离的最大值为9.故选C.
①选3+4,5,7作为三角形,则三边长为7,5,7.7-5<7<7+5,能构成三角形,此时两个螺丝间的最长距离为7;
②选4+5,3,7作为三角形,则三边长为9,3,7.7-3<9<7+3,能构成三角形,此时两个螺丝间的最大距离为9;
③选3+7,4,5作为三角形,则三边长为10,4,5.4+5<10,不能构成三角形,此种情况不成立;
④选5+7,3,4作为三角形,则三边长为12,3,4.而3+4<12,不能构成三角形,此种情况不成立.
综上所述,任两螺丝的距离的最大值为9.故选C.
6. 把一条长 15 厘米的线段截成三段,使每条线段的长度都是整数,用三条线段可以组成
7
个不同的三角形.答案:7 [解析]根据三角形三边关系,三条线段可以组成三角形的有:①1,7,7;②2,6,7;③3,5,7;④3,6,6;⑤4,5,6;⑥5,5,5;⑦4,4,7.故可以组成7个不同的三角形.
7. (教材 P6 练习 T3·变式)在△ABC 中,若∠C 为钝角,则在该三角形中的最大边是
AB
.答案:AB
8. 如图,已知 P 是△ABC 内一点,试说明$ PA+PB+PC>\frac{1}{2}(AB+BC+AC).$
]

]

答案:已知在△ABP中,AP+BP>AB.
同理可得BP+PC>BC,AP+PC>AC.
以上三式分别相加,得2(PA+PB+PC)>AB+BC+AC,即PA+PB+PC>$\frac{1}{2}(AB+BC+AC)$.
同理可得BP+PC>BC,AP+PC>AC.
以上三式分别相加,得2(PA+PB+PC)>AB+BC+AC,即PA+PB+PC>$\frac{1}{2}(AB+BC+AC)$.
9. (2025·河北唐山路南区期中)使用 a,b 两根直的铁丝做成一个三角形框架,尺寸如图所示,若需要将其中一根铁丝折成两段,则可以把铁丝分为两段的是(

A.只有 a
B.只有 b
C.a,b 都可以
D.a,b 都不可以
]
B
). 
A.只有 a
B.只有 b
C.a,b 都可以
D.a,b 都不可以
]
答案:B [解析]
∵a<b,
∴由三角形三边关系定理得到:只有将铁丝b折成两段才能做成一个三角形框架.故选B.
∵a<b,
∴由三角形三边关系定理得到:只有将铁丝b折成两段才能做成一个三角形框架.故选B.
10. (2024·安徽合肥庐阳区期末)如图,从点 A 到点 G,下列路径最短的是(

A.A→B→F→G
B.A→C→F→G
C.A→D→F→G
D.A→E→F→G
]
A
). 
A.A→B→F→G
B.A→C→F→G
C.A→D→F→G
D.A→E→F→G
]
答案:A [解析]根据三角形两边之和大于第三边可知A→B→F→G路径最短.故选A.
11. 如图是一个直三棱柱的表面展开图,其中 AD= 10,CD= 2,则下列可作为 AB 长度的是(
A.5
B.4
C.3
D.2
B
).A.5
B.4
C.3
D.2
答案:B [解析]由题图可知,AD=AB+BC+CD.
∵AD=10,CD=2,
∴AB+BC=8.设AB=x,则BC=8-x.由三角形三边关系,得$\left\{\begin{array}{l} 8-x<x+2,\\ 8-x>x-2,\end{array}\right.$解得3<x<5,
∴AB的长度可以是4.故选B.
方法论 解答本题时需要根据题图得出AD=AB+BC+CD,再根据AD=10,CD=2,得出AB+BC=8,然后设AB=x,得出BC=8-x,最后根据三角形的三边关系列出不等式组,求得AB的取值范围,然后求出问题的答案.
∵AD=10,CD=2,
∴AB+BC=8.设AB=x,则BC=8-x.由三角形三边关系,得$\left\{\begin{array}{l} 8-x<x+2,\\ 8-x>x-2,\end{array}\right.$解得3<x<5,
∴AB的长度可以是4.故选B.
方法论 解答本题时需要根据题图得出AD=AB+BC+CD,再根据AD=10,CD=2,得出AB+BC=8,然后设AB=x,得出BC=8-x,最后根据三角形的三边关系列出不等式组,求得AB的取值范围,然后求出问题的答案.