1. 用含有字母的式子表示下面的数量关系。
(1) 比 $ a $ 少 $ 5.4 $。
(2) 比 $ x $ 的 $ 7 $ 倍多 $ 5 $。
(3) $ x $ 与 $ y $ 的和的 $ 4 $ 倍。
(4) $ x $ 的平方减去 $ y $ 个 $ 8 $。
(1) 比 $ a $ 少 $ 5.4 $。
(2) 比 $ x $ 的 $ 7 $ 倍多 $ 5 $。
(3) $ x $ 与 $ y $ 的和的 $ 4 $ 倍。
(4) $ x $ 的平方减去 $ y $ 个 $ 8 $。
答案：(1) $a - 5.4$
(2) $7x + 5$
(3) $4(x + y)$
(4) $x^2 - 8y$
(2) $7x + 5$
(3) $4(x + y)$
(4) $x^2 - 8y$
2. 每筐苹果 $ x$ kg,每筐梨 $ y$ kg。
(1) $ 2y $ 表示：
(2) $ x - y $ 表示：
(3) $ 3(x + y) $ 表示：
(1) $ 2y $ 表示：
2筐梨的重量
(2) $ x - y $ 表示：
每筐苹果比每筐梨多的重量
(3) $ 3(x + y) $ 表示：
3筐苹果和3筐梨的总重量（或3筐苹果与梨各1筐组合共3组的总重量）
答案：(1) $2y$ 表示：$2$ 筐梨的重量
(2) $x - y$ 表示：每筐苹果比每筐梨多的重量
(3) $3(x + y)$ 表示：$3$ 筐苹果和$ 3$ 筐梨的总重量（或$ 3$ 筐苹果与梨各$ 1$ 筐组合共$ 3$ 组的总重量 ）
(2) $x - y$ 表示：每筐苹果比每筐梨多的重量
(3) $3(x + y)$ 表示：$3$ 筐苹果和$ 3$ 筐梨的总重量（或$ 3$ 筐苹果与梨各$ 1$ 筐组合共$ 3$ 组的总重量 ）
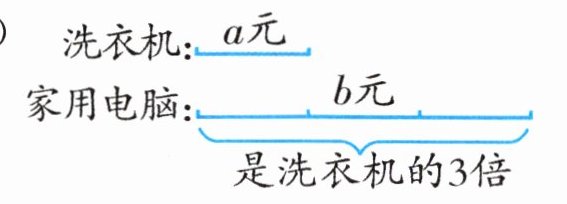
3. 看图列方程。
(2)$3a=$
1. (1)$m=$$n - x$
；$n=$$m + x$
(2)$3a=$
$a + b$
；$a=$$\frac{a + b}{3}$
；$\frac{a + b}{a}$
$=3$答案：1. 对于第一小题：
已知$x = n - m$，根据等式的性质：
由$x = n - m$，移项可得$m=n - x$（等式两边同时加$m$再减$x$）；
由$x = n - m$，移项可得$n=m + x$（等式两边同时加$m$）。
2. 对于第二小题：
已知家用电脑价格是洗衣机的$3$倍，洗衣机$a$元，家用电脑$b$元。
因为家用电脑价格$=$洗衣机价格$×3$，所以$3a=a + b$（从图中可知家用电脑价格比洗衣机价格多$b$元，且是洗衣机价格的$3$倍）；
由$3a=a + b$，移项可得$b = 3a−a=2a$，再根据$3a=a + b$，等式两边同时除以$3$得$a=\frac{a + b}{3}$；
因为家用电脑价格$÷$洗衣机价格$ = 3$，所以$\frac{a + b}{a}=3$。
故答案依次为：(1)$n - x$；$m + x$；(2)$a + b$；$\frac{a + b}{3}$；$\frac{a + b}{a}$。
已知$x = n - m$，根据等式的性质：
由$x = n - m$，移项可得$m=n - x$（等式两边同时加$m$再减$x$）；
由$x = n - m$，移项可得$n=m + x$（等式两边同时加$m$）。
2. 对于第二小题：
已知家用电脑价格是洗衣机的$3$倍，洗衣机$a$元，家用电脑$b$元。
因为家用电脑价格$=$洗衣机价格$×3$，所以$3a=a + b$（从图中可知家用电脑价格比洗衣机价格多$b$元，且是洗衣机价格的$3$倍）；
由$3a=a + b$，移项可得$b = 3a−a=2a$，再根据$3a=a + b$，等式两边同时除以$3$得$a=\frac{a + b}{3}$；
因为家用电脑价格$÷$洗衣机价格$ = 3$，所以$\frac{a + b}{a}=3$。
故答案依次为：(1)$n - x$；$m + x$；(2)$a + b$；$\frac{a + b}{3}$；$\frac{a + b}{a}$。
4. 小兰计划 $ a $ 天看完一本书。
(1) 小兰实际用
(2) 这本书的总页数是
(3) 当 $ a = 10 $,$ b = 1 $ 时,这本书一共有多少页？
(1) 小兰实际用
$a - b$
天看完。(2) 这本书的总页数是
$12(a - b)$页
。(3) 当 $ a = 10 $,$ b = 1 $ 时,这本书一共有多少页？
当$a = 10$，$b = 1$时，把数值代入$12(a - b)$可得：$12×(10 - 1)=12×9 = 108$（页）答：这本书一共有108页。
答案：（1）从图中可知计划$a$天看完，实际提前$b$天看完，那么实际用天数为$(a - b)$天。
（2）因为实际每天看$12$页，实际看了$(a - b)$天，根据“总页数 = 每天看的页数×天数”，可得这本书总页数为$12(a - b)$页。
（3）当$a = 10$，$b = 1$时，把数值代入$12(a - b)$可得：
$12×(10 - 1)=12×9 = 108$（页）
答：（1）$a - b$；（2）$12(a - b)$页；（3）这本书一共有$108$页。
（2）因为实际每天看$12$页，实际看了$(a - b)$天，根据“总页数 = 每天看的页数×天数”，可得这本书总页数为$12(a - b)$页。
（3）当$a = 10$，$b = 1$时，把数值代入$12(a - b)$可得：
$12×(10 - 1)=12×9 = 108$（页）
答：（1）$a - b$；（2）$12(a - b)$页；（3）这本书一共有$108$页。