1. 在$-(-8)$,$|-1|$,$-|0|$,$(-2)^3$这四个数中,负数有(
A.1个
B.2个
C.3个
D.4个
A
)A.1个
B.2个
C.3个
D.4个
答案:A
解析:
$-(-8)=8$,$|-1|=1$,$-|0|=0$,$(-2)^3=-8$,负数有1个。
A
A
2. 下列各组代数式中,为同类项的是(
A.$3x^2y与-3xy^2$
B.$5xy与-\frac{1}{2}yx$
C.$4xyz与4xy$
D.$2x与2x^2$
B
)A.$3x^2y与-3xy^2$
B.$5xy与-\frac{1}{2}yx$
C.$4xyz与4xy$
D.$2x与2x^2$
答案:B
解析:
同类项是指所含字母相同,并且相同字母的指数也相同的项。
A选项:$3x^2y$与$-3xy^2$,$x$的指数分别为2和1,$y$的指数分别为1和2,指数不同,不是同类项。
B选项:$5xy$与$-\frac{1}{2}yx$,所含字母都是$x$、$y$,且$x$、$y$的指数均为1,是同类项。
C选项:$4xyz$含有字母$x$、$y$、$z$,$4xy$含有字母$x$、$y$,所含字母不同,不是同类项。
D选项:$2x$与$2x^2$,$x$的指数分别为1和2,指数不同,不是同类项。
B
A选项:$3x^2y$与$-3xy^2$,$x$的指数分别为2和1,$y$的指数分别为1和2,指数不同,不是同类项。
B选项:$5xy$与$-\frac{1}{2}yx$,所含字母都是$x$、$y$,且$x$、$y$的指数均为1,是同类项。
C选项:$4xyz$含有字母$x$、$y$、$z$,$4xy$含有字母$x$、$y$,所含字母不同,不是同类项。
D选项:$2x$与$2x^2$,$x$的指数分别为1和2,指数不同,不是同类项。
B
3. 解方程$\frac{x+1}{2}= \frac{4}{3}x+1$,下列去分母的过程正确的是(
A.$3(x+1)= 8x+1$
B.$3(x+1)= 4x+6$
C.$x+1= 8x+6$
D.$3(x+1)= 8x+6$
D
)A.$3(x+1)= 8x+1$
B.$3(x+1)= 4x+6$
C.$x+1= 8x+6$
D.$3(x+1)= 8x+6$
答案:D
解析:
方程两边同乘6,得$3(x+1)=8x+6$。
D
D
4. 已知$x= 2是关于x的方程\frac{5}{2}x-2a= 0$的解,则代数式$2a-1$的值是(
A.3
B.4
C.5
D.6
B
)A.3
B.4
C.5
D.6
答案:B
解析:
将$x = 2$代入方程$\frac{5}{2}x - 2a = 0$,得$\frac{5}{2}×2 - 2a = 0$,即$5 - 2a = 0$,解得$2a = 5$,则$2a - 1 = 5 - 1 = 4$。
B
B
5. 数轴上表示整数的点称为整点. 某数轴的单位长度为1 cm,若在这条数轴上任意画一条长为10 cm的线段AB,则线段AB在数轴上盖住的整点个数是(
A.8或9
B.9或10
C.10或11
D.11或12
C
)A.8或9
B.9或10
C.10或11
D.11或12
答案:C
解析:
当线段AB的端点在整点时,盖住的整点个数为$10 + 1=11$个;
当线段AB的端点不在整点时,盖住的整点个数为10个。
综上,线段AB在数轴上盖住的整点个数是10或11。
C
当线段AB的端点不在整点时,盖住的整点个数为10个。
综上,线段AB在数轴上盖住的整点个数是10或11。
C
6. 已知$\alpha$,$\beta$是两个钝角,计算$\frac{1}{6}(\alpha+\beta)$的值,甲、乙、丙、丁四位同学算出了四种不同的答案,分别为$24^\circ$,$48^\circ$,$76^\circ$,$86^\circ$. 其中,只有一个答案是正确的,正确的答案是(
A.$24^\circ$
B.$48^\circ$
C.$60^\circ$
D.$72^\circ$
B
)A.$24^\circ$
B.$48^\circ$
C.$60^\circ$
D.$72^\circ$
答案:B
解析:
因为$\alpha$,$\beta$是两个钝角,所以$90^\circ < \alpha < 180^\circ$,$90^\circ < \beta < 180^\circ$。
则$90^\circ + 90^\circ < \alpha + \beta < 180^\circ + 180^\circ$,即$180^\circ < \alpha + \beta < 360^\circ$。
两边同时除以$6$,得$\frac{180^\circ}{6} < \frac{1}{6}(\alpha + \beta) < \frac{360^\circ}{6}$,即$30^\circ < \frac{1}{6}(\alpha + \beta) < 60^\circ$。
在给出的答案$24^\circ$,$48^\circ$,$76^\circ$,$86^\circ$中,只有$48^\circ$在此范围内。
B
则$90^\circ + 90^\circ < \alpha + \beta < 180^\circ + 180^\circ$,即$180^\circ < \alpha + \beta < 360^\circ$。
两边同时除以$6$,得$\frac{180^\circ}{6} < \frac{1}{6}(\alpha + \beta) < \frac{360^\circ}{6}$,即$30^\circ < \frac{1}{6}(\alpha + \beta) < 60^\circ$。
在给出的答案$24^\circ$,$48^\circ$,$76^\circ$,$86^\circ$中,只有$48^\circ$在此范围内。
B
7. 平方得$\frac{16}{25}$的数是
$\frac{4}{5},-\frac{4}{5}$
;立方等于本身的数是$1,-1$和0
.答案:$\frac{4}{5},-\frac{4}{5};1,-1$和0
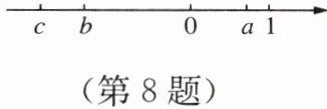
8. 有理数$a$,$b$,$c$在数轴上表示如图所示,用“>”“<”或“=”填空:$a+c$
<
0,$abc$>
0.
答案:$<,>$
解析:
由数轴可知:$c < b < 0 < a < 1$,且$|c| > |a|$。
对于$a + c$:因为$c$为负数,$a$为正数,且负数的绝对值大于正数的绝对值,所以$a + c < 0$。
对于$abc$:$a$为正数,$b$、$c$为负数,两个负数相乘得正数,正数再与正数相乘仍为正数,所以$abc > 0$。
$<$,$>$
对于$a + c$:因为$c$为负数,$a$为正数,且负数的绝对值大于正数的绝对值,所以$a + c < 0$。
对于$abc$:$a$为正数,$b$、$c$为负数,两个负数相乘得正数,正数再与正数相乘仍为正数,所以$abc > 0$。
$<$,$>$
9. 如果$x-y= 2$,那么$4-x+y= $
2
.答案:2
解析:
$4 - x + y = 4 - (x - y)$,因为$x - y = 2$,所以$4 - (x - y) = 4 - 2 = 2$。
2
2
10. 已知代数式$3x-12$的值与$-\frac{1}{3}$互为倒数,则$x$的值是
3
.答案:3
解析:
因为代数式$3x - 12$的值与$-\frac{1}{3}$互为倒数,所以$(3x - 12) × (-\frac{1}{3}) = 1$。
方程两边同时乘以$-3$得:$3x - 12 = -3$。
移项得:$3x = -3 + 12$。
计算得:$3x = 9$。
两边同时除以$3$得:$x = 3$。
3
方程两边同时乘以$-3$得:$3x - 12 = -3$。
移项得:$3x = -3 + 12$。
计算得:$3x = 9$。
两边同时除以$3$得:$x = 3$。
3
11. 一个角的余角与这个角的补角也互为补角,这个角为
$45^{\circ}$
.答案:$45^{\circ}$
解析:
设这个角为$x$,则它的余角为$90^{\circ}-x$,补角为$180^{\circ}-x$。
因为这个角的余角与补角互为补角,所以$(90^{\circ}-x)+(180^{\circ}-x)=180^{\circ}$
$270^{\circ}-2x=180^{\circ}$
$-2x=180^{\circ}-270^{\circ}$
$-2x=-90^{\circ}$
$x=45^{\circ}$
$45^{\circ}$
因为这个角的余角与补角互为补角,所以$(90^{\circ}-x)+(180^{\circ}-x)=180^{\circ}$
$270^{\circ}-2x=180^{\circ}$
$-2x=180^{\circ}-270^{\circ}$
$-2x=-90^{\circ}$
$x=45^{\circ}$
$45^{\circ}$
12. 数轴上点$A$,$B分别表示数-5.5和-10.5$,$C是AB$的中点,点$C$所表示的数是
-8
.答案:-8
解析:
$\frac{-5.5 + (-10.5)}{2} = \frac{-16}{2} = -8$
13. 若$|x-1|+(y+2)^2= 0$,则$(x+y)^3= $
-1
.答案:-1
解析:
因为$|x - 1| \geq 0$,$(y + 2)^2 \geq 0$,且$|x - 1| + (y + 2)^2 = 0$,所以$|x - 1| = 0$,$(y + 2)^2 = 0$。
由$|x - 1| = 0$,得$x - 1 = 0$,解得$x = 1$。
由$(y + 2)^2 = 0$,得$y + 2 = 0$,解得$y = -2$。
则$x + y = 1 + (-2) = -1$,所以$(x + y)^3 = (-1)^3 = -1$。
-1
由$|x - 1| = 0$,得$x - 1 = 0$,解得$x = 1$。
由$(y + 2)^2 = 0$,得$y + 2 = 0$,解得$y = -2$。
则$x + y = 1 + (-2) = -1$,所以$(x + y)^3 = (-1)^3 = -1$。
-1
14. 顺次标有5,10,15,20,25,…的卡片若干张,如果其中相邻三张卡片上所标的数的和为180,那么这三张卡片所标的数分别为
55
,60
,65
.答案:55, 60, 65
解析:
设中间的数为$5n$,则前一个数为$5(n-1)$,后一个数为$5(n+1)$。
$5(n-1)+5n+5(n+1)=180$
$5n - 5 + 5n + 5n + 5 = 180$
$15n = 180$
$n = 12$
前一个数:$5(n-1)=5×11=55$
中间数:$5n=5×12=60$
后一个数:$5(n+1)=5×13=65$
55, 60, 65
$5(n-1)+5n+5(n+1)=180$
$5n - 5 + 5n + 5n + 5 = 180$
$15n = 180$
$n = 12$
前一个数:$5(n-1)=5×11=55$
中间数:$5n=5×12=60$
后一个数:$5(n+1)=5×13=65$
55, 60, 65