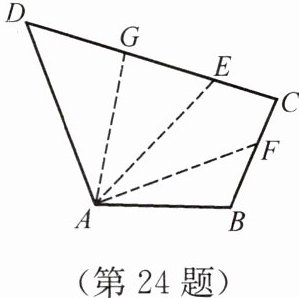
24. 任意拿一张四边形纸片$ABCD$(如图),按如下方式折叠:先过点$A随意折出一道折痕AE$,再分别把$AB$,$AD都折叠到与AE$重叠的位置,折痕分别为$AF和AG$. 此时$\angle FAG与\angle BAD$有怎样的数量关系?为什么?

答案:$∠FAG=\frac{1}{2}∠BAD$. 理由如下:因为$∠BAE+∠DAE=∠BAD,∠FAE=\frac{1}{2}∠BAE,∠GAE=\frac{1}{2}∠DAE$,所以$∠FAG=∠FAE+∠GAE=\frac{1}{2}∠BAE+\frac{1}{2}∠DAE=\frac{1}{2}(∠BAE+∠DAE)=\frac{1}{2}∠BAD$
解析:
$\angle FAG=\frac{1}{2}\angle BAD$. 理由如下:因为$\angle BAE + \angle DAE = \angle BAD$,由折叠性质得$\angle FAE = \frac{1}{2}\angle BAE$,$\angle GAE = \frac{1}{2}\angle DAE$,所以$\angle FAG = \angle FAE + \angle GAE = \frac{1}{2}\angle BAE + \frac{1}{2}\angle DAE = \frac{1}{2}(\angle BAE + \angle DAE) = \frac{1}{2}\angle BAD$.
25. 某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元. 厂方在开展促销活动期间,向客户提供两种优惠方案:①买一套西装送一条领带;②西装和领带都按定价的90%付款. 现有某客户要到该服装厂购买西装20套,领带$x$条($x>20$).
(1)若该客户按方案①购买,需付款
(2)若$x= 30$,通过计算说明此时按哪种方案购买较为合算.
(3)当$x= 30$时,有没有更为省钱的购买方案呢?如有,请写出你设计的方案.
解:(2)方案①:40x+3200=40×30+3200=4400(元)
方案②:36x+3600=36×30+3600=4680(元)
4400<4680
答:此时按方案①购买较为合算.
(3)先按方案①买西装20套,领带20条,再按方案②买领带10条,这样所花费用最少.
(1)若该客户按方案①购买,需付款
40x + 3200
元;若该客户按方案②购买,需付款36x + 3600
元.(用含$x$的代数式表示)(2)若$x= 30$,通过计算说明此时按哪种方案购买较为合算.
(3)当$x= 30$时,有没有更为省钱的购买方案呢?如有,请写出你设计的方案.
解:(2)方案①:40x+3200=40×30+3200=4400(元)
方案②:36x+3600=36×30+3600=4680(元)
4400<4680
答:此时按方案①购买较为合算.
(3)先按方案①买西装20套,领带20条,再按方案②买领带10条,这样所花费用最少.
答案:
$(1) 40x + 3200,36x + 3600$
$(1) 40x + 3200,36x + 3600$
解:$(2)$方案$①$:$40x+3200=40×30+3200=4400($元$)$
方案$②$:$36x+3600=36×30+3600=4680($元$)$
$4400<4680$
答:此时按方案$①$购买较为合算$.$
$(3)$先按方案$①$买西装$20$套,领带$20$条,再按方案$②$买领带$10$条,这样所花费用最少$.$
26. 如图①,某校七年级数学学习小组在课后综合实践活动中,把三角板$AOB的直角顶点O放在互相垂直的两条直线PQ$,$MN的垂足O$处,并使两条直角边落在直线$PQ$,$MN$上,将$\triangle AOB绕点O顺时针旋转\alpha$($0^\circ<\alpha<180^\circ$).
(1)如图②,若$\alpha=26^\circ$,则$\angle BOP= $
(2)若射线$OC是\angle BOM$的平分线,且$\angle POC= \beta$.
① 若$\triangle AOB$旋转到图③的位置,则$\angle BON$的度数为多少?(用含$\beta$的代数式表示)
② 在$\triangle AOB$旋转的过程中,若$\angle AOC= 2\angle AOM$,求此时$\beta$的值.
(1)如图②,若$\alpha=26^\circ$,则$\angle BOP= $
$64$
°,$\angle AOM+\angle BOQ= $$180$
°.(2)若射线$OC是\angle BOM$的平分线,且$\angle POC= \beta$.
① 若$\triangle AOB$旋转到图③的位置,则$\angle BON$的度数为多少?(用含$\beta$的代数式表示)
$2\beta$
② 在$\triangle AOB$旋转的过程中,若$\angle AOC= 2\angle AOM$,求此时$\beta$的值.
$β = 60^{\circ}$或$36^{\circ}$
答案:
(1) $64^{\circ},180^{\circ}$. 因为$MN⊥PQ$,所以$∠POM=∠QOM=90^{\circ}$,因为$∠BOM=∠AOQ=26^{\circ}$,所以$∠BOP=90^{\circ}-26^{\circ}=64^{\circ}$;因为$∠AOB=90^{\circ}$,所以$∠AOM+∠BOQ=∠AOM+∠AOQ+∠AOB=∠QOM+∠AOB=90^{\circ}+90^{\circ}=180^{\circ}$
(2) ① 2β. 因为$∠POM=90^{\circ},∠POC=β$,所以$∠COM=90^{\circ}-β$,因为射线OC是$∠BOM$的平分线,所以$∠BOM=2∠COM=180^{\circ}-2β$,所以$∠BON=180^{\circ}-(180^{\circ}-2β)=2β$ ② $β = 60^{\circ}$或$36^{\circ}$. 当OA位于$∠QOM$内部时,因为OC平分$∠BOM$,所以$∠BOC=∠COM$,因为$∠AOC=2∠AOM$,所以$∠AOM=∠COM$,所以$∠AOM=∠COM=∠BOC=\frac{1}{3}∠AOB$,因为$∠AOB=90^{\circ}$,所以$∠COM=30^{\circ}$,所以$β=90^{\circ}-30^{\circ}=60^{\circ}$;当OA位于$∠POM$内部时,如图,因为$∠POM=90^{\circ},∠POC=β$,所以$∠COM=90^{\circ}-β$,因为OC平分$∠BOM$,所以$∠BOM=2∠COM=180^{\circ}-2β,∠BOC=∠COM=90^{\circ}-β$,所以$∠AOM=180^{\circ}-2β-90^{\circ}=90^{\circ}-2β,∠AOC=∠AOB-∠BOC=90^{\circ}-(90^{\circ}-β)=β$,因为$∠AOC=2∠AOM$,所以$β=2(90^{\circ}-2β)$,解得$β = 36^{\circ}$. 综上所述,若$∠AOC=2∠AOM$,则β的值为$60^{\circ}$或$36^{\circ}$
(1) $64^{\circ},180^{\circ}$. 因为$MN⊥PQ$,所以$∠POM=∠QOM=90^{\circ}$,因为$∠BOM=∠AOQ=26^{\circ}$,所以$∠BOP=90^{\circ}-26^{\circ}=64^{\circ}$;因为$∠AOB=90^{\circ}$,所以$∠AOM+∠BOQ=∠AOM+∠AOQ+∠AOB=∠QOM+∠AOB=90^{\circ}+90^{\circ}=180^{\circ}$
(2) ① 2β. 因为$∠POM=90^{\circ},∠POC=β$,所以$∠COM=90^{\circ}-β$,因为射线OC是$∠BOM$的平分线,所以$∠BOM=2∠COM=180^{\circ}-2β$,所以$∠BON=180^{\circ}-(180^{\circ}-2β)=2β$ ② $β = 60^{\circ}$或$36^{\circ}$. 当OA位于$∠QOM$内部时,因为OC平分$∠BOM$,所以$∠BOC=∠COM$,因为$∠AOC=2∠AOM$,所以$∠AOM=∠COM$,所以$∠AOM=∠COM=∠BOC=\frac{1}{3}∠AOB$,因为$∠AOB=90^{\circ}$,所以$∠COM=30^{\circ}$,所以$β=90^{\circ}-30^{\circ}=60^{\circ}$;当OA位于$∠POM$内部时,如图,因为$∠POM=90^{\circ},∠POC=β$,所以$∠COM=90^{\circ}-β$,因为OC平分$∠BOM$,所以$∠BOM=2∠COM=180^{\circ}-2β,∠BOC=∠COM=90^{\circ}-β$,所以$∠AOM=180^{\circ}-2β-90^{\circ}=90^{\circ}-2β,∠AOC=∠AOB-∠BOC=90^{\circ}-(90^{\circ}-β)=β$,因为$∠AOC=2∠AOM$,所以$β=2(90^{\circ}-2β)$,解得$β = 36^{\circ}$. 综上所述,若$∠AOC=2∠AOM$,则β的值为$60^{\circ}$或$36^{\circ}$