9. 魔术师说:“请你任想一个两位数,将十位数字乘2,然后加3,将所得新数乘5,最后将得到的数加个位数字,只要告诉我计算结果,我就能知道你心里想的两位数.”请你解释这个魔术背后的数学道理.
答案:设这个数为$\overline{ab}$,则计算结果为$(2a+3)×5+b=10a+b+15$,只要将结果减15,就得到$10a+b$,即为原来的两位数
解析:
设这个两位数的十位数字为$a$,个位数字为$b$,则这个两位数为$10a + b$。
计算过程为:$(2a + 3)×5 + b$,展开得$10a + 15 + b$,即$10a + b + 15$。
所以,用计算结果减去$15$,可得$10a + b$,即原来的两位数。
计算过程为:$(2a + 3)×5 + b$,展开得$10a + 15 + b$,即$10a + b + 15$。
所以,用计算结果减去$15$,可得$10a + b$,即原来的两位数。
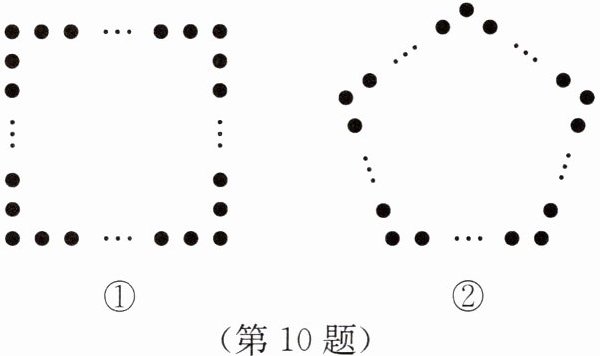
10. (1)如图①,正方形的每条边上都有$n$个棋子,图①中共有多少个棋子?
(2)如图②,正五边形(五条边相等的五边形)的每条边上都有$n$个棋子,图②比图①多几个棋子?
(3)正$m$边形(每条边都相等的$m$边形)的每条边上都有$n$个棋子,则共有多少个棋子?
(2)如图②,正五边形(五条边相等的五边形)的每条边上都有$n$个棋子,图②比图①多几个棋子?
(3)正$m$边形(每条边都相等的$m$边形)的每条边上都有$n$个棋子,则共有多少个棋子?

答案:
解:$(1)$图$①$中共有$4(n-1)$个棋子$.$
$(2)$图$②$中有$5(n-1)$个棋子,
图$②$比图$①$中多$5(n-1)-4(n-1)=(n-1)$个棋子$.$
$(3)$正$m $边形共有$m(n-1)$个棋子$.$
11. 课堂上,老师设计了一个数学游戏,给甲、乙、丙三名同学各一张写有代数式(已化简)的卡片,若两位同学的代数式相减等于第三位同学的代数式,则游戏成功.甲、乙、丙的卡片如图所示,其中丙的卡片有一部分看不清楚了(图中阴影所示).


(1)计算甲的代数式减乙的代数式的结果,并判断该运算能否使游戏成功;
(2)小明发现丙的代数式减甲的代数式可以使游戏成功,请求出丙的代数式.
答案:
解:$(1)$甲$-$乙$=2a^2+4ab+3-(-\frac 12a^2-6ab+9)=2a^2+4ab+3+\frac 12a^2+6ab-9$
$=\frac 52a^2+10ab-6.$
因为丙为$+12,$
所以游戏不成功$.$
$(2)$由题意得丙$-$甲$=$乙,
所以丙$=$甲$+$乙$=2a^2+4ab+3+(-\frac 12a^2-6ab+9)=2a^2+4ab+3-\frac 12a^2-6ab+9$
$=\frac 32a^2-2ab+12 .$
故丙的代数是为$\frac 32a^2-2ab+12 .$