8. 如图,指出图中物体分别是由哪些几何体组成的。①②③
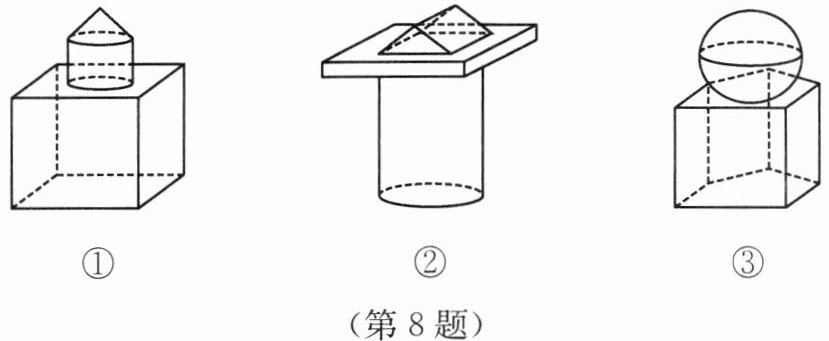

答案:① 是由一个正方体、一个圆柱体、一个圆锥体组成的组合体 ② 是由一个圆柱体、一个长方体、一个三棱柱组成的组合体 ③ 是由一个五棱柱、一个球体组成的组合体
9. 如图,至少找出下列几何体的四个共同点。


答案:答案不唯一,如:都由平面组成,侧面都是长方形,都有上下底面,都有侧棱等
10. 如图①所示的几何体叫三棱柱,它有6个顶点、9条棱、5个面,如图②和图③所示的几何体分别是四棱柱和五棱柱。①②③(1)四棱柱有

8
个顶点,12
条棱,6
个面。(2)五棱柱有10
个顶点,15
条棱,7
个面。(3)你能由此猜想六棱柱、七棱柱各有几个顶点、几条棱、几个面吗?n棱柱呢?
猜想:六棱柱有12个顶点、18条棱、8个面;七棱柱有14个顶点、21条棱、9个面;n棱柱有2n个顶点、3n条棱、(n+2)个面
答案:
(1)8,12,6
(2)10,15,7
(3)猜想:六棱柱有 12 个顶点、18 条棱、8 个面;七棱柱有 14 个顶点、21 条棱、9 个面;n 棱柱有 2n 个顶点、3n 条棱、(n+2)个面
(1)8,12,6
(2)10,15,7
(3)猜想:六棱柱有 12 个顶点、18 条棱、8 个面;七棱柱有 14 个顶点、21 条棱、9 个面;n 棱柱有 2n 个顶点、3n 条棱、(n+2)个面
11. 如图,①②③④四个图形都是平面图形,观察图形和表中对应的数值,探究计数的方法并解答下面的问题。


(1)数一数每个图形各有多少个顶点、多少条边,这些边围出多少个区域,将结果填入右上表;
(2)根据表格,猜想平面图形的顶点数、边数和区域数之间的关系;
(3)如果一个平面图形有20个顶点和11个区域,那么这个平面图形有几条边?


(1)数一数每个图形各有多少个顶点、多少条边,这些边围出多少个区域,将结果填入右上表;
①:4,6,3,③:8,12,5,④:10,15,6
(2)根据表格,猜想平面图形的顶点数、边数和区域数之间的关系;
V+F=E+1
(3)如果一个平面图形有20个顶点和11个区域,那么这个平面图形有几条边?
30
答案:
(1)①:4,6,3,③:8,12,5,④:10,15,6
(2)V+F=E+1
(3)根据
(2)的关系式,得该平面图形有 30 条边
(1)①:4,6,3,③:8,12,5,④:10,15,6
(2)V+F=E+1
(3)根据
(2)的关系式,得该平面图形有 30 条边