6. 如图,正方形ABCD的边长为a,E,F分别是对角线BD上的两点,过点E,F分别作AD,AB的平行线,则图中阴影部分的面积之和为
$\frac{1}{2}a^{2}$
.答案:$\frac{1}{2}a^{2}$
解析:
设过点E作AD的平行线交AB于点M,过点F作AB的平行线交AD于点N,交BC于点P,过点E作AB的平行线交BC于点Q。
因为四边形ABCD是正方形,边长为$a$,BD是对角线,所以$\angle ABD = \angle ADB = 45^\circ$。
设$AM = x$,则$ME = x$(等腰直角三角形),阴影部分中上方矩形面积为$x \cdot a$;设$BP = y$,则$PF = y$,阴影部分中下方矩形面积为$y \cdot (a - x)$。
由图形可知$x + y = a$,阴影部分总面积为$x \cdot a + y \cdot (a - x) = ax + ay - xy$,又因为$y = a - x$,代入得$ax + a(a - x) - x(a - x) = ax + a^2 - ax - ax + x^2 = a^2 - ax + x^2$,此方法复杂。
换用割补法,将阴影部分平移拼接,可组成一个长为$a$,宽为$\frac{a}{2}$的矩形,故面积为$\frac{1}{2}a^2$。
$\frac{1}{2}a^{2}$
因为四边形ABCD是正方形,边长为$a$,BD是对角线,所以$\angle ABD = \angle ADB = 45^\circ$。
设$AM = x$,则$ME = x$(等腰直角三角形),阴影部分中上方矩形面积为$x \cdot a$;设$BP = y$,则$PF = y$,阴影部分中下方矩形面积为$y \cdot (a - x)$。
由图形可知$x + y = a$,阴影部分总面积为$x \cdot a + y \cdot (a - x) = ax + ay - xy$,又因为$y = a - x$,代入得$ax + a(a - x) - x(a - x) = ax + a^2 - ax - ax + x^2 = a^2 - ax + x^2$,此方法复杂。
换用割补法,将阴影部分平移拼接,可组成一个长为$a$,宽为$\frac{a}{2}$的矩形,故面积为$\frac{1}{2}a^2$。
$\frac{1}{2}a^{2}$
7. 如图①,将边长为10 cm的正方形纸片做成七巧板,并用这副七巧板拼成“温暖小屋”(图②),则图中阴影部分的面积是
25
cm².答案:25
解析:
正方形边长为$10\,cm$,其面积为$10×10 = 100\,cm^2$。
七巧板中,阴影部分为小正方形。原正方形面积被分成$16$个小等腰直角三角形(每个小三角形面积相等),小正方形由$4$个小三角形组成。
每个小三角形面积为$\frac{100}{16} = \frac{25}{4}\,cm^2$,则阴影部分面积为$4×\frac{25}{4} = 25\,cm^2$。
$25$
七巧板中,阴影部分为小正方形。原正方形面积被分成$16$个小等腰直角三角形(每个小三角形面积相等),小正方形由$4$个小三角形组成。
每个小三角形面积为$\frac{100}{16} = \frac{25}{4}\,cm^2$,则阴影部分面积为$4×\frac{25}{4} = 25\,cm^2$。
$25$
8. 分析图①②④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分.


答案:
如图
如图

9. 如图所示的三角形纸片的三边长分别为12 cm,16 cm,20 cm,请你用两张这样的纸片拼出各种三角形或四边形,并指出周长最长为多少.
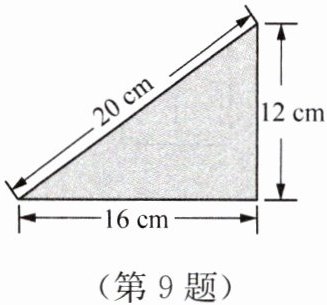

答案:72 cm
解析:
拼三角形情况
以12cm边重合:周长为$16 + 20 + 16 + 20 = 72\,cm$
以16cm边重合:周长为$12 + 20 + 12 + 20 = 64\,cm$
以20cm边重合:周长为$12 + 16 + 12 + 16 = 56\,cm$
拼四边形情况
以12cm边重合:周长为$16 + 20 + 16 + 20 = 72\,cm$
以16cm边重合:周长为$12 + 20 + 12 + 20 = 64\,cm$
以20cm边重合:周长为$12 + 16 + 12 + 16 = 56\,cm$
周长最长为$72\,cm$
以12cm边重合:周长为$16 + 20 + 16 + 20 = 72\,cm$
以16cm边重合:周长为$12 + 20 + 12 + 20 = 64\,cm$
以20cm边重合:周长为$12 + 16 + 12 + 16 = 56\,cm$
拼四边形情况
以12cm边重合:周长为$16 + 20 + 16 + 20 = 72\,cm$
以16cm边重合:周长为$12 + 20 + 12 + 20 = 64\,cm$
以20cm边重合:周长为$12 + 16 + 12 + 16 = 56\,cm$
周长最长为$72\,cm$
10. 如图是某设计师设计的方桌布图案的一部分,请你运用旋转变换的方法,在方格纸上将该图形绕点O按顺时针方向依次旋转90°,180°,270°,并画出它变换后的图形. 你会得到一个美丽的图形,快来试一试吧!


答案:

