1. 如果OC是$\angle AOB$的平分线,那么
∠AOC=∠BOC=$\frac{1}{2}$∠AOB
.答案:∠AOC=∠BOC=$\frac{1}{2}$∠AOB
2. 对于任意的$\angle \alpha和\angle \beta,$可能的大小关系是
∠α<∠β,∠α=∠β,∠α>∠β
.答案:∠α<∠β,∠α=∠β,∠α>∠β
解析:
$\angle \alpha < \angle \beta$,$\angle \alpha = \angle \beta$,$\angle \alpha > \angle \beta$
3. 图中的黑色球
能
(填“能”或“不能”)被击入右下角的袋中.(先估测,再用直尺和圆规作出反射角加以检验)答案:能
4. 如图,$\angle AOB= 20°,$$\angle BOC= 80°,$OE是$\angle AOC$的平分线,则$\angle COE$的大小是(
A.50°
B.40°
C.30°
D.20°
A
)A.50°
B.40°
C.30°
D.20°
答案:A
解析:
解:
$\angle AOC = \angle AOB + \angle BOC = 20^\circ + 80^\circ = 100^\circ$
∵OE是$\angle AOC$的平分线
∴$\angle COE = \frac{1}{2}\angle AOC = \frac{1}{2} × 100^\circ = 50^\circ$
A
$\angle AOC = \angle AOB + \angle BOC = 20^\circ + 80^\circ = 100^\circ$
∵OE是$\angle AOC$的平分线
∴$\angle COE = \frac{1}{2}\angle AOC = \frac{1}{2} × 100^\circ = 50^\circ$
A
5. 已知OC是$\angle AOB$内的一条射线,下列条件中不能确定OC是$\angle AOB的平分线的是(
C
)A. \angle AOC= \angle BOC B. \angle AOB= 2\angle AOCC. \angle AOC+\angle COB= \angle AOB D. \angle BOC= \frac{1}{2}\angle AOB$答案:C
6. 把一副三角板按如图所示方式拼在一起,作$\angle ABE$的平分线BM,则$\angle EBM$的大小是(
A.30°
B.90°
C.60°
D.75°
C
)A.30°
B.90°
C.60°
D.75°
答案:C
7. 如图,直线AB,CD相交于点O,OE平分$\angle AOD,OF$平分$\angle BOD. $当直线CD绕点O顺时针旋转$\alpha°(0<\alpha<180)$时,下列各角的度数与$\angle BOD$变化无关的是( )
C
$A. \angle AOD B. \angle AOC C. \angle EOF D. \angle DOF$答案:C
解析:
设$\angle BOD = x$。
$\angle AOD = 180^\circ - x$,与$x$有关;
$\angle AOC = \angle BOD = x$,与$x$有关;
OE平分$\angle AOD$,则$\angle DOE = \frac{1}{2}\angle AOD = \frac{1}{2}(180^\circ - x) = 90^\circ - \frac{x}{2}$;
OF平分$\angle BOD$,则$\angle DOF = \frac{1}{2}\angle BOD = \frac{x}{2}$,与$x$有关;
$\angle EOF = \angle DOE + \angle DOF = (90^\circ - \frac{x}{2}) + \frac{x}{2} = 90^\circ$,与$x$无关。
C
$\angle AOD = 180^\circ - x$,与$x$有关;
$\angle AOC = \angle BOD = x$,与$x$有关;
OE平分$\angle AOD$,则$\angle DOE = \frac{1}{2}\angle AOD = \frac{1}{2}(180^\circ - x) = 90^\circ - \frac{x}{2}$;
OF平分$\angle BOD$,则$\angle DOF = \frac{1}{2}\angle BOD = \frac{x}{2}$,与$x$有关;
$\angle EOF = \angle DOE + \angle DOF = (90^\circ - \frac{x}{2}) + \frac{x}{2} = 90^\circ$,与$x$无关。
C
8. 已知$\angle AOB= 80°,OC$平分$\angle AOB,$若$\angle BOD= 20°,$则$\angle COD= $
20°或60°
.答案:20°或60°
解析:
∵OC平分∠AOB,∠AOB=80°,
∴∠BOC=∠AOC=$\frac{1}{2}$∠AOB=40°。
情况1:OD在∠AOB内部,
∠COD=∠BOC - ∠BOD=40° - 20°=20°。
情况2:OD在∠AOB外部,
∠COD=∠BOC + ∠BOD=40° + 20°=60°。
20°或60°
9. 如图,$\angle BOD= 118°,$$\angle COD$是直角,OC平分$\angle AOB,则\angle AOB=
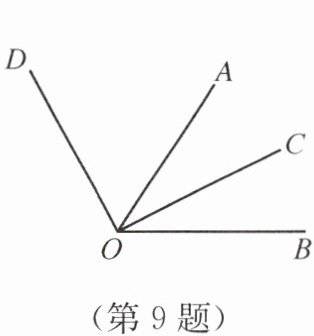
56
°.$
答案:56
解析:
∵∠COD是直角,
∴∠COD=90°,
∵∠BOD=118°,
∴∠BOC=∠BOD - ∠COD=118° - 90°=28°,
∵OC平分∠AOB,
∴∠AOB=2∠BOC=2×28°=56°。
56