1. 两条相交直线所成的四个角中,有
公共顶点
没有公共边
的两个角叫作对顶角.答案:公共顶点,公共边
2. 两条直线相交,对顶角
相等
.答案:相等
3. 下列各图中,∠1与∠2是对顶角的是(
B
)答案:B
4. 如图,直线AB与CD相交于点O,若∠1= 120°,则∠2+∠3=
120
°.答案:120
解析:
∵直线AB与CD相交于点O,∠1=120°
∴∠2=∠3(对顶角相等)
∠1+∠3=180°(邻补角互补)
∴∠3=180°-∠1=180°-120°=60°
∴∠2+∠3=60°+60°=120°
120
5. 如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC= 70°,则∠BOD=
35
°.答案:35
解析:
∵OA平分∠EOC,∠EOC=70°,
∴∠AOC=∠AOE=∠EOC×$\frac{1}{2}$=70°×$\frac{1}{2}$=35°,
∵∠AOC与∠BOD是对顶角,
∴∠BOD=∠AOC=35°。
35
6. 如图,a,b,c三条直线相交于一点,则∠1+∠2+∠3等于(
A.180°
B.120°
C.90°
D.不能确定
A
)A.180°
B.120°
C.90°
D.不能确定
答案:A
解析:
由对顶角相等可知,∠1的对顶角与∠1相等,∠2的对顶角与∠2相等,∠3的对顶角与∠3相等。
因为三条直线相交于一点,形成的六个角之和为360°,所以∠1+∠2+∠3=360°÷2=180°。
A
因为三条直线相交于一点,形成的六个角之和为360°,所以∠1+∠2+∠3=360°÷2=180°。
A
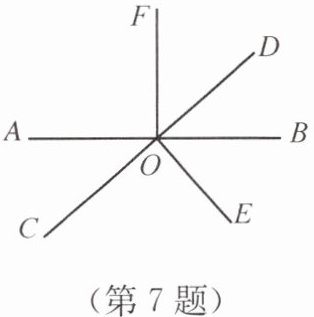
7. 如图,直线AB与CD相交于点O,∠EOC= ∠AOF= 90°,∠DOF与∠AOE的关系是(
A.互余
B.互补
C.相等
D.和是钝角
B
) 
A.互余
B.互补
C.相等
D.和是钝角
答案:B
解析:
∵∠AOF=90°,∠EOC=90°,
又
∵∠AOC=∠BOD(对顶角相等),
∠DOF=∠AOF+∠AOD=90°+∠AOD,
∠AOE=∠EOC+∠AOC=90°+∠AOC=90°+∠BOD,
∵∠AOD+∠BOD=180°(邻补角定义),
∴∠DOF+∠AOE=90°+∠AOD+90°+∠BOD=180°+(∠AOD+∠BOD)=180°+180°=360°。
答案:B
8. 如图,直线DE与BC相交于点O,∠COE与∠AOE互余,∠BOD= 35°,则∠AOE=
55
°.答案:55
解析:
∵直线DE与BC相交于点O,
∴∠COE=∠BOD=35°(对顶角相等).
∵∠COE与∠AOE互余,
∴∠COE+∠AOE=90°,
∴∠AOE=90°-∠COE=90°-35°=55°.
55