1. 下列长度的各组线段中,能围成直角三角形的是 (
A.1,1,2
B.1,2,3
C.1,$\sqrt{2}$,$\sqrt{3}$
D.2,3,4
C
)A.1,1,2
B.1,2,3
C.1,$\sqrt{2}$,$\sqrt{3}$
D.2,3,4
答案:C
解析:
A. $1^2 + 1^2 = 2$, $2^2 = 4$, $2 \neq 4$, 不能围成直角三角形;
B. $1^2 + 2^2 = 5$, $3^2 = 9$, $5 \neq 9$, 不能围成直角三角形;
C. $1^2 + (\sqrt{2})^2 = 1 + 2 = 3$, $(\sqrt{3})^2 = 3$, $3 = 3$, 能围成直角三角形;
D. $2^2 + 3^2 = 13$, $4^2 = 16$, $13 \neq 16$, 不能围成直角三角形;
C
B. $1^2 + 2^2 = 5$, $3^2 = 9$, $5 \neq 9$, 不能围成直角三角形;
C. $1^2 + (\sqrt{2})^2 = 1 + 2 = 3$, $(\sqrt{3})^2 = 3$, $3 = 3$, 能围成直角三角形;
D. $2^2 + 3^2 = 13$, $4^2 = 16$, $13 \neq 16$, 不能围成直角三角形;
C
2. 如图,A,C两棵树之间隔有一湖,在与AC方向成$90^{\circ}$角的CB方向上的点B处测得AB= 50 m,BC= 40 m,则A,C两棵树之间的距离为 (
A.30 m
B.40 m
C.50 m
D.60 m
A
)A.30 m
B.40 m
C.50 m
D.60 m
答案:A
解析:
在$Rt\triangle ABC$中,$\angle ACB=90^{\circ}$,$AB=50\ m$,$BC=40\ m$。
由勾股定理得:$AC^{2}+BC^{2}=AB^{2}$
$AC^{2}=AB^{2}-BC^{2}=50^{2}-40^{2}=2500 - 1600=900$
$AC=\sqrt{900}=30\ m$
A
由勾股定理得:$AC^{2}+BC^{2}=AB^{2}$
$AC^{2}=AB^{2}-BC^{2}=50^{2}-40^{2}=2500 - 1600=900$
$AC=\sqrt{900}=30\ m$
A
3. 如图,直线上有三个正方形A,B,C,若正方形A,B的面积分别为5和11,则正方形C的面积是 (
A.6
B.5
C.11
D.16
A
)A.6
B.5
C.11
D.16
答案:A
解析:
设正方形A、B、C的边长分别为$a$、$b$、$c$。
由题意得:$a^2=5$,$b^2=11$。
观察图形,正方形A、B、C构成的三角形为直角三角形,其中正方形B的边长为斜边,正方形A、C的边长为两直角边。
根据勾股定理:$a^2 + c^2 = b^2$。
则$c^2 = b^2 - a^2 = 11 - 5 = 6$。
故正方形C的面积是6。
A
由题意得:$a^2=5$,$b^2=11$。
观察图形,正方形A、B、C构成的三角形为直角三角形,其中正方形B的边长为斜边,正方形A、C的边长为两直角边。
根据勾股定理:$a^2 + c^2 = b^2$。
则$c^2 = b^2 - a^2 = 11 - 5 = 6$。
故正方形C的面积是6。
A
4. 在Rt△ABC中,$\angle C= 90^{\circ}$,$\angle A$,$\angle B$,$\angle C$的对边分别是a,b,c,若a+b= 14,c= 10,则Rt△ABC的面积是 (
A.24
B.36
C.48
D.60
A
)A.24
B.36
C.48
D.60
答案:A
解析:
在Rt△ABC中,∠C=90°,由勾股定理得$a^2 + b^2 = c^2$。已知$c=10$,则$a^2 + b^2 = 10^2 = 100$。
因为$a + b = 14$,所以$(a + b)^2 = 14^2 = 196$,即$a^2 + 2ab + b^2 = 196$。
将$a^2 + b^2 = 100$代入上式,得$100 + 2ab = 196$,解得$2ab = 96$,$ab = 48$。
Rt△ABC的面积是$\frac{1}{2}ab = \frac{1}{2} × 48 = 24$。
A
因为$a + b = 14$,所以$(a + b)^2 = 14^2 = 196$,即$a^2 + 2ab + b^2 = 196$。
将$a^2 + b^2 = 100$代入上式,得$100 + 2ab = 196$,解得$2ab = 96$,$ab = 48$。
Rt△ABC的面积是$\frac{1}{2}ab = \frac{1}{2} × 48 = 24$。
A
5. 如图,方格纸中最长的线段是 (
A.AB
B.BC
C.CD
D.AE
B
)A.AB
B.BC
C.CD
D.AE
答案:B
解析:
设每个小方格边长为1。
AB:横向3格,纵向2格,长度为$\sqrt{3^2+2^2}=\sqrt{13}$;
BC:横向3格,纵向3格,长度为$\sqrt{3^2+3^2}=3\sqrt{2}$;
CD:横向2格,纵向1格,长度为$\sqrt{2^2+1^2}=\sqrt{5}$;
AE:横向1格,纵向3格,长度为$\sqrt{1^2+3^2}=\sqrt{10}$。
比较得$3\sqrt{2}$最大,即BC最长。
B
AB:横向3格,纵向2格,长度为$\sqrt{3^2+2^2}=\sqrt{13}$;
BC:横向3格,纵向3格,长度为$\sqrt{3^2+3^2}=3\sqrt{2}$;
CD:横向2格,纵向1格,长度为$\sqrt{2^2+1^2}=\sqrt{5}$;
AE:横向1格,纵向3格,长度为$\sqrt{1^2+3^2}=\sqrt{10}$。
比较得$3\sqrt{2}$最大,即BC最长。
B
6. 如图,$\angle ABC= 90^{\circ}$,CB= 4,AC= 5,则阴影部分的面积是
$\frac{9\pi}{8}$
.答案:$\frac{9\pi}{8}$
解析:
在$Rt\triangle ABC$中,$\angle ABC=90^{\circ}$,$AC=5$,$CB=4$,由勾股定理得$AB=\sqrt{AC^{2}-BC^{2}}=\sqrt{5^{2}-4^{2}}=3$。
阴影部分为以$AB$为直径的半圆,半径$r=\frac{AB}{2}=\frac{3}{2}$。
其面积$S=\frac{1}{2}\pi r^{2}=\frac{1}{2}\pi×(\frac{3}{2})^{2}=\frac{9\pi}{8}$。
$\frac{9\pi}{8}$
阴影部分为以$AB$为直径的半圆,半径$r=\frac{AB}{2}=\frac{3}{2}$。
其面积$S=\frac{1}{2}\pi r^{2}=\frac{1}{2}\pi×(\frac{3}{2})^{2}=\frac{9\pi}{8}$。
$\frac{9\pi}{8}$
7. 一个直角三角形的两边长分别是3和7,则第三边长的平方为
58或40
.答案:58或40
解析:
当3和7为直角边时,第三边长的平方为$3^{2}+7^{2}=9 + 49=58$;
当7为斜边,3为直角边时,第三边长的平方为$7^{2}-3^{2}=49 - 9=40$。
58或40
当7为斜边,3为直角边时,第三边长的平方为$7^{2}-3^{2}=49 - 9=40$。
58或40
8. 《九章算术》中记载了一道“折竹”问题:“今有竹高一丈,末折抵地,去根四尺,问折者高几何?”题意是:一根竹子原高1丈(1丈= 10尺),中部有一处折断,竹梢触地面处离竹根4尺,试问折断处离地面
4.2
尺高.答案:4.2
解析:
设折断处离地面$x$尺高,则折断部分长为$(10 - x)$尺。
根据勾股定理可得:$x^2 + 4^2=(10 - x)^2$
展开得:$x^2 + 16 = 100 - 20x + x^2$
移项化简得:$20x = 84$
解得:$x=\frac{84}{20}=\frac{21}{5}=4.2$
4.2
根据勾股定理可得:$x^2 + 4^2=(10 - x)^2$
展开得:$x^2 + 16 = 100 - 20x + x^2$
移项化简得:$20x = 84$
解得:$x=\frac{84}{20}=\frac{21}{5}=4.2$
4.2
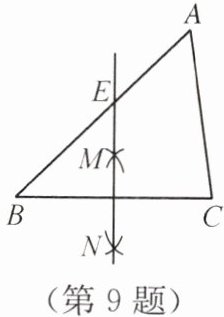
9. 如图,在△ABC中,按以下步骤作图:① 分别以点B和C为圆心,以大于$\frac{1}{2}BC$的长为半径作弧,两弧相交于点M和N;② 作直线MN,交边AB于点E. 若AC= 5,BE= 4,$\angle B= 45^{\circ}$,则AB的长为______
7
.
答案:7
解析:
连接EC。
由作图知,MN垂直平分BC,故EB=EC=4。
所以∠ECB=∠B=45°,则∠AEC=∠B+∠ECB=90°。
在Rt△AEC中,AE=$\sqrt{AC^2-EC^2}=\sqrt{5^2-4^2}=3$。
AB=AE+BE=3+4=7。
7
由作图知,MN垂直平分BC,故EB=EC=4。
所以∠ECB=∠B=45°,则∠AEC=∠B+∠ECB=90°。
在Rt△AEC中,AE=$\sqrt{AC^2-EC^2}=\sqrt{5^2-4^2}=3$。
AB=AE+BE=3+4=7。
7