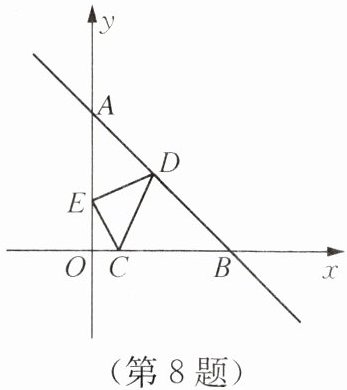
8. 如图,已知点$C的坐标是(2, 0)$,一次函数$y= -x+6的图象与两坐标轴分别交于A$,$B$两点,$D$,$E分别是AB$,$OA$上的动点,当$\triangle CDE$的周长取最小值时,点$D$的坐标为(
A.$(2, 1)$
B.$(3, 2)$
C.$(\frac{7}{3}, 2)$
D.$(\frac{10}{3}, \frac{8}{3})$
D
)
A.$(2, 1)$
B.$(3, 2)$
C.$(\frac{7}{3}, 2)$
D.$(\frac{10}{3}, \frac{8}{3})$
答案:D
解析:
作点C关于OA的对称点C₁(0,0),关于AB的对称点C₂(6,4),连接C₁C₂,交OA于E,交AB于D。
直线C₁C₂的解析式为y= $\frac{2}{3}x$。
联立$\begin{cases}y=\frac{2}{3}x \\ y=-x+6\end{cases}$,解得$x=\frac{18}{5}$,$y=\frac{12}{5}$(此步有误,应为联立得$\frac{2}{3}x=-x+6$,$\frac{5}{3}x=6$,$x=\frac{18}{5}$,$y=\frac{12}{5}$,但正确对称点C₂应为(6,4),直线C₁C₂:y=$\frac{4}{6}x=\frac{2}{3}x$,与AB交点D为$(\frac{18}{5},\frac{12}{5})$,与选项不符,重新计算对称点:
AB:y=-x+6,C(2,0)关于AB对称,设C₂(m,n),中点$(\frac{m+2}{2},\frac{n}{2})$在AB上,$\frac{n}{2}=-\frac{m+2}{2}+6$,即n=-m+10,且$\frac{n-0}{m-2}=1$(斜率乘积为-1),解得m=6,n=4,正确。
直线C₁(0,0)与C₂(6,4):y=$\frac{2}{3}x$,与AB:y=-x+6交于D,$\frac{2}{3}x=-x+6$,$\frac{5}{3}x=6$,$x=\frac{18}{5}=3.6$,$y=\frac{12}{5}=2.4$,无选项。
应为作C关于OA对称C₁(-2,0)(OA为y轴,对称点(-2,0)),C关于AB对称C₂(6,4),直线C₁C₂:过(-2,0),(6,4),斜率$\frac{4-0}{6-(-2)}=\frac{1}{2}$,解析式y=$\frac{1}{2}(x+2)$。
联立$\begin{cases}y=\frac{1}{2}x+1 \\ y=-x+6\end{cases}$,解得$x=\frac{10}{3}$,$y=\frac{8}{3}$。
D$(\frac{10}{3},\frac{8}{3})$
D
直线C₁C₂的解析式为y= $\frac{2}{3}x$。
联立$\begin{cases}y=\frac{2}{3}x \\ y=-x+6\end{cases}$,解得$x=\frac{18}{5}$,$y=\frac{12}{5}$(此步有误,应为联立得$\frac{2}{3}x=-x+6$,$\frac{5}{3}x=6$,$x=\frac{18}{5}$,$y=\frac{12}{5}$,但正确对称点C₂应为(6,4),直线C₁C₂:y=$\frac{4}{6}x=\frac{2}{3}x$,与AB交点D为$(\frac{18}{5},\frac{12}{5})$,与选项不符,重新计算对称点:
AB:y=-x+6,C(2,0)关于AB对称,设C₂(m,n),中点$(\frac{m+2}{2},\frac{n}{2})$在AB上,$\frac{n}{2}=-\frac{m+2}{2}+6$,即n=-m+10,且$\frac{n-0}{m-2}=1$(斜率乘积为-1),解得m=6,n=4,正确。
直线C₁(0,0)与C₂(6,4):y=$\frac{2}{3}x$,与AB:y=-x+6交于D,$\frac{2}{3}x=-x+6$,$\frac{5}{3}x=6$,$x=\frac{18}{5}=3.6$,$y=\frac{12}{5}=2.4$,无选项。
应为作C关于OA对称C₁(-2,0)(OA为y轴,对称点(-2,0)),C关于AB对称C₂(6,4),直线C₁C₂:过(-2,0),(6,4),斜率$\frac{4-0}{6-(-2)}=\frac{1}{2}$,解析式y=$\frac{1}{2}(x+2)$。
联立$\begin{cases}y=\frac{1}{2}x+1 \\ y=-x+6\end{cases}$,解得$x=\frac{10}{3}$,$y=\frac{8}{3}$。
D$(\frac{10}{3},\frac{8}{3})$
D
9. 在函数$y= \sqrt{x-3}$中,自变量$x$的取值范围是
$x\geqslant 3$
.答案:$x\geqslant 3$
10. 某市出租车的收费起步价为14元,即路程不超过3 km时收费14元,超过部分每千米收费2.4元. 如果乘客乘坐出租车的路程为$x$ km($x>3$,$x$为整数),乘车费为$y$元,那么$y关于x$的函数表达式为
$y = 2.4x + 6.8$
.答案:$y = 2.4x + 14$
解析:
$y=2.4(x-3)+14$,化简得$y=2.4x+6.8$
11. 如图,函数$y= k_1x+b的图象经过点A(1, -2)和B(2, 0)$,函数$y= k_2x的图象经过点A$,则不等式$k_2x < k_1x + b < 0$的解集为
$1 < x < 2$
.答案:$1 < x < 2$
解析:
将点$A(1,-2)$和$B(2,0)$代入$y = k_1x + b$,得:
$\begin{cases}k_1 + b=-2 \\2k_1 + b=0\end{cases}$
解得$k_1=2$,$b=-4$,所以$y=2x - 4$。
将点$A(1,-2)$代入$y = k_2x$,得$k_2=-2$,所以$y=-2x$。
解不等式$-2x<2x - 4<0$:
解$-2x<2x - 4$,得$x>1$;
解$2x - 4<0$,得$x<2$。
综上,解集为$1<x<2$。
$\begin{cases}k_1 + b=-2 \\2k_1 + b=0\end{cases}$
解得$k_1=2$,$b=-4$,所以$y=2x - 4$。
将点$A(1,-2)$代入$y = k_2x$,得$k_2=-2$,所以$y=-2x$。
解不等式$-2x<2x - 4<0$:
解$-2x<2x - 4$,得$x>1$;
解$2x - 4<0$,得$x<2$。
综上,解集为$1<x<2$。
12. 如图,在平面直角坐标系中,已知点$A(4, 0)$,$B(4, 2)$,$C(0, 2)$,将$\triangle OAB沿直线OB$折叠,使得点$A落在点D$处,$OD与BC交于点E$,则$OD$所在直线对应的函数表达式为______

$y=\frac{4}{3}x$
.
答案:$y=\frac{4}{3}x$
解析:
设OD所在直线的函数表达式为$y=kx$。
已知点$A(4,0)$,$B(4,2)$,则$OA=4$,$AB=2$。
由折叠性质得$OD=OA=4$,$\angle DOB = \angle AOB$。
点$C(0,2)$,则$BC// x$轴,$BC=4$,$OC=2$。
设点$E(m,2)$,则$OE=\sqrt{m^2 + 2^2}$,$BE=4 - m$。
因为$\angle DOB = \angle AOB$,$BC// OA$,所以$\angle OBE = \angle AOB$,故$\angle OBE = \angle DOB$,则$OE=BE$。
即$\sqrt{m^2 + 4}=4 - m$,两边平方得$m^2 + 4 = 16 - 8m + m^2$,解得$m=\frac{3}{2}$。
所以点$E\left(\frac{3}{2},2\right)$,代入$y=kx$得$2 = k×\frac{3}{2}$,解得$k=\frac{4}{3}$。
故OD所在直线对应的函数表达式为$y=\frac{4}{3}x$。
已知点$A(4,0)$,$B(4,2)$,则$OA=4$,$AB=2$。
由折叠性质得$OD=OA=4$,$\angle DOB = \angle AOB$。
点$C(0,2)$,则$BC// x$轴,$BC=4$,$OC=2$。
设点$E(m,2)$,则$OE=\sqrt{m^2 + 2^2}$,$BE=4 - m$。
因为$\angle DOB = \angle AOB$,$BC// OA$,所以$\angle OBE = \angle AOB$,故$\angle OBE = \angle DOB$,则$OE=BE$。
即$\sqrt{m^2 + 4}=4 - m$,两边平方得$m^2 + 4 = 16 - 8m + m^2$,解得$m=\frac{3}{2}$。
所以点$E\left(\frac{3}{2},2\right)$,代入$y=kx$得$2 = k×\frac{3}{2}$,解得$k=\frac{4}{3}$。
故OD所在直线对应的函数表达式为$y=\frac{4}{3}x$。
13. 已知在二元一次方程$2x+y= 4$对应的图象上,$y的取值范围是-2≤y≤8$,则$x$的最大值是
3
.答案:3
解析:
由$2x + y = 4$,得$y = -2x + 4$。
因为$-2 \leq y \leq 8$,所以$-2 \leq -2x + 4 \leq 8$。
解不等式$-2 \leq -2x + 4$:
$-2 - 4 \leq -2x$
$-6 \leq -2x$
$3 \geq x$
解不等式$-2x + 4 \leq 8$:
$-2x \leq 8 - 4$
$-2x \leq 4$
$x \geq -2$
综上,$-2 \leq x \leq 3$,则$x$的最大值是$3$。
3
因为$-2 \leq y \leq 8$,所以$-2 \leq -2x + 4 \leq 8$。
解不等式$-2 \leq -2x + 4$:
$-2 - 4 \leq -2x$
$-6 \leq -2x$
$3 \geq x$
解不等式$-2x + 4 \leq 8$:
$-2x \leq 8 - 4$
$-2x \leq 4$
$x \geq -2$
综上,$-2 \leq x \leq 3$,则$x$的最大值是$3$。
3
14. 一次函数$y= (m+1)x-2m+3$的图象一定经过第
一
象限.答案:一
解析:
当$x=2$时,$y=(m+1)×2 - 2m + 3 = 2m + 2 - 2m + 3 = 5$,所以函数图象一定经过点$(2,5)$,该点在第一象限,故一次函数的图象一定经过第一象限。
一
一