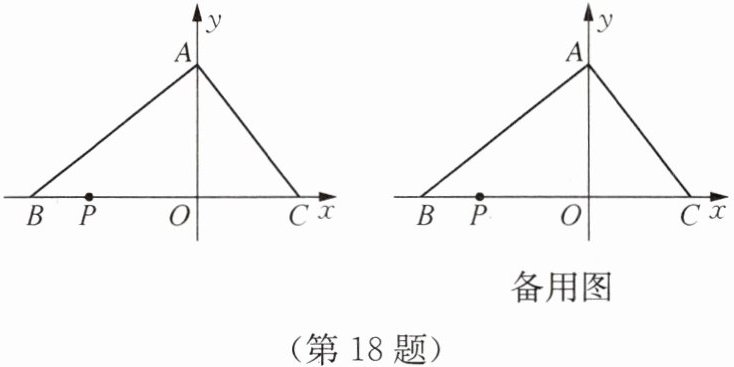
18. 如图,在平面直角坐标系中,$O$为坐标原点. $\triangle ABC的边BC在x$轴上,$A$,$B$,$C三点的坐标分别为A(0, m)$,$B(-5, 0)$,$C(n, 0)$,且$(n-3)^2+\sqrt{3m-12}= 0$,点$P从点B$出发,以每秒2个单位长度的速度沿射线$BO$匀速运动,设点$P运动的时间为t$ s.
(1) 求$A$,$C$两点的坐标.______
(2) 连接$PA$,设$\triangle POA的面积为S$,请写出$S关于t$的函数表达式.______
(3) 当点$P在线段BO$上运动时,是否存在某一位置,使$\triangle PAC$是等腰三角形?若存在,请求出满足条件的所有点$P的坐标以及此时对应的t$的值;若不存在,请说明理由.______
(1) 求$A$,$C$两点的坐标.______
(2) 连接$PA$,设$\triangle POA的面积为S$,请写出$S关于t$的函数表达式.______
(3) 当点$P在线段BO$上运动时,是否存在某一位置,使$\triangle PAC$是等腰三角形?若存在,请求出满足条件的所有点$P的坐标以及此时对应的t$的值;若不存在,请说明理由.______

答案:
(1)
∵ $(n - 3)^{2}+\sqrt{3m - 12}=0$,
∴ $n - 3 = 0$,$3m - 12 = 0$,$n = 3$,$m = 4$,
∴ 点 A 的坐标是 $(0,4)$,点 C 的坐标是 $(3,0)$。
(2)
∵ 点 B 的坐标是 $(-5,0)$,
∴ $OB = 5$。
① 当 $0\leqslant t<\frac{5}{2}$ 时,点 P 在线段 OB 上,如图①,
∵ $OP = 5 - 2t$,$OA = 4$,
∴ $\triangle POA$ 的面积 $S=\frac{1}{2}× OP× AO=\frac{1}{2}× (5 - 2t)× 4 = 10 - 4t$;
② 当 $t=\frac{5}{2}$ 时,点 P 和点 O 重合,此时 $\triangle APO$ 不存在,即 $S = 0$;
③ 当 $t>\frac{5}{2}$ 时,点 P 在射线 OC 上,如图②,
∵ $OP = 2t - 5$,$OA = 4$,
∴ $\triangle POA$ 的面积 $S=\frac{1}{2}× OP× AO=\frac{1}{2}× (2t - 5)× 4 = 4t - 10$。
综上,$S=\begin{cases}10 - 4t(0\leqslant t<\frac{5}{2}) \\ 0(t=\frac{5}{2}) \\ 4t - 10(t>\frac{5}{2})\end{cases}$
(3) 分三种情况:
① $\angle PAC$ 为顶角时,即 $AP = AC$,
∴ AO 为 $\triangle PAC$ 中垂线,
∴ $PO = CO = 3$,
∴ 点 P 的坐标为 $(-3,0)$,
∴ $t=\frac{BP}{2}=1$;
② $\angle ACP$ 为顶角时,$AC = CP$,根据勾股定理,得 $AC=\sqrt{OC^{2}+OA^{2}} = 5$,
∴ $PO = 2$ 或 8(舍弃),
∴ 点 P 的坐标为 $(-2,0)$,
∴ $t=\frac{BP}{2}=1.5$;
③ $\angle APC$ 为顶角时,$AP = PC$,设 $PA = x$,根据勾股定理,在 $Rt\triangle PAO$ 中,$x^{2}=(x - 3)^{2}+4^{2}$,解得 $x=\frac{25}{6}$,
∴ $PO=\frac{25}{6}-3=\frac{7}{6}$,
∴ 点 P 的坐标为 $(-\frac{7}{6},0)$,
∴ $t=\frac{BP}{2}=\frac{23}{12}$。
综上,点 P 的坐标为 $(-3,0)$,$(-2,0)$,$(-\frac{7}{6},0)$,对应的时间分别是 $t = 1$,$1.5$,$\frac{23}{12}$。
(1)
∵ $(n - 3)^{2}+\sqrt{3m - 12}=0$,
∴ $n - 3 = 0$,$3m - 12 = 0$,$n = 3$,$m = 4$,
∴ 点 A 的坐标是 $(0,4)$,点 C 的坐标是 $(3,0)$。
(2)
∵ 点 B 的坐标是 $(-5,0)$,
∴ $OB = 5$。
① 当 $0\leqslant t<\frac{5}{2}$ 时,点 P 在线段 OB 上,如图①,
∵ $OP = 5 - 2t$,$OA = 4$,
∴ $\triangle POA$ 的面积 $S=\frac{1}{2}× OP× AO=\frac{1}{2}× (5 - 2t)× 4 = 10 - 4t$;
② 当 $t=\frac{5}{2}$ 时,点 P 和点 O 重合,此时 $\triangle APO$ 不存在,即 $S = 0$;
③ 当 $t>\frac{5}{2}$ 时,点 P 在射线 OC 上,如图②,
∵ $OP = 2t - 5$,$OA = 4$,
∴ $\triangle POA$ 的面积 $S=\frac{1}{2}× OP× AO=\frac{1}{2}× (2t - 5)× 4 = 4t - 10$。
综上,$S=\begin{cases}10 - 4t(0\leqslant t<\frac{5}{2}) \\ 0(t=\frac{5}{2}) \\ 4t - 10(t>\frac{5}{2})\end{cases}$
(3) 分三种情况:
① $\angle PAC$ 为顶角时,即 $AP = AC$,
∴ AO 为 $\triangle PAC$ 中垂线,
∴ $PO = CO = 3$,
∴ 点 P 的坐标为 $(-3,0)$,
∴ $t=\frac{BP}{2}=1$;
② $\angle ACP$ 为顶角时,$AC = CP$,根据勾股定理,得 $AC=\sqrt{OC^{2}+OA^{2}} = 5$,
∴ $PO = 2$ 或 8(舍弃),
∴ 点 P 的坐标为 $(-2,0)$,
∴ $t=\frac{BP}{2}=1.5$;
③ $\angle APC$ 为顶角时,$AP = PC$,设 $PA = x$,根据勾股定理,在 $Rt\triangle PAO$ 中,$x^{2}=(x - 3)^{2}+4^{2}$,解得 $x=\frac{25}{6}$,
∴ $PO=\frac{25}{6}-3=\frac{7}{6}$,
∴ 点 P 的坐标为 $(-\frac{7}{6},0)$,
∴ $t=\frac{BP}{2}=\frac{23}{12}$。
综上,点 P 的坐标为 $(-3,0)$,$(-2,0)$,$(-\frac{7}{6},0)$,对应的时间分别是 $t = 1$,$1.5$,$\frac{23}{12}$。
19. 一辆快车和一辆慢车在相距16 km的$A$,$B$两站点间往返载客,两车均在每天早上8:00从$A$站出发,快车中途不停靠,慢车仅在$A$,$B两站的中点C$站停上下客. 设两车行驶速度不变,在各站点停靠时长相同,两车与$A站的距离为s$ km,经过的时间为$t$ min,上午发车后慢车第一个往返期间两车行驶情况如图所示.
(1) 求慢车、快车的速度和它们第一次停靠的时长.______
(2) 求慢车和快车出发后第一次相遇时它们与$A$站的距离.______
(3) 慢车和快车第一次相遇后,经过多少时间两车再次相遇?______

(1) 求慢车、快车的速度和它们第一次停靠的时长.______
(2) 求慢车和快车出发后第一次相遇时它们与$A$站的距离.______
(3) 慢车和快车第一次相遇后,经过多少时间两车再次相遇?______

答案:
(1) 根据题意,得慢车速度为 $\frac{8}{12}=\frac{2}{3}(km/min)$,快车速度为 $\frac{16}{12}=\frac{4}{3}(km/min)$,它们第一次停靠的时长为 $\frac{72 - 2× 24}{3}=8(min)$。
(2) 由题意,得当 $20\leqslant t\leqslant 32$ 时,慢车和快车第一次相遇,分别设慢车和快车的函数表达式为 $s = kt + B(k\neq 0)$,$s = k_{1}t + B_{1}(k_{1}\neq 0)$,由
(1)可得慢车对应的函数图象经过 $(20,8)$,$(32,16)$,快车对应的函数图象经过 $(20,16)$,$(32,0)$,分别代入函数表达式后,可得 $\begin{cases}8 = 20k + b \\ 16 = 32k + b\end{cases}$,$\begin{cases}16 = 20k_{1} + b_{1} \\ 0 = 32k_{1} + b_{1}\end{cases}$,解得 $\begin{cases}k=\frac{2}{3} \\ b = -\frac{16}{3}\end{cases}$,$\begin{cases}k_{1}=-\frac{4}{3} \\ b_{1}=\frac{128}{3}\end{cases}$。
慢车离 A 站的路程 s 关于 t 的函数表达式为 $s=\frac{2}{3}t-\frac{16}{3}$,快车离 A 站的路程 s 关于 t 的函数表达式为 $s=-\frac{4}{3}t+\frac{128}{3}$,联立两式 $\begin{cases}s=\frac{2}{3}t-\frac{16}{3} \\ s=-\frac{4}{3}t+\frac{128}{3}\end{cases}$,解得 $\begin{cases}t = 24 \\ s=\frac{32}{3}\end{cases}$,即第一次相遇时与 A 站的距离为 $\frac{32}{3}km$。
(3) 由
(2),得 $t_{1}=12 + 8 + 4 = 24$,由题意可得函数图象关于过点 $(36,0)$ 且垂直于横轴的直线对称,$P_{1}$,$P_{2}$ 是一组对称点,所以 $t_{2}-36 = 36 - t_{1}$,解得 $t_{2}=48$,$t_{2}-t_{1}=24$。所以第一次相遇后,经过 24 min 后两车再次相遇。
(1) 根据题意,得慢车速度为 $\frac{8}{12}=\frac{2}{3}(km/min)$,快车速度为 $\frac{16}{12}=\frac{4}{3}(km/min)$,它们第一次停靠的时长为 $\frac{72 - 2× 24}{3}=8(min)$。
(2) 由题意,得当 $20\leqslant t\leqslant 32$ 时,慢车和快车第一次相遇,分别设慢车和快车的函数表达式为 $s = kt + B(k\neq 0)$,$s = k_{1}t + B_{1}(k_{1}\neq 0)$,由
(1)可得慢车对应的函数图象经过 $(20,8)$,$(32,16)$,快车对应的函数图象经过 $(20,16)$,$(32,0)$,分别代入函数表达式后,可得 $\begin{cases}8 = 20k + b \\ 16 = 32k + b\end{cases}$,$\begin{cases}16 = 20k_{1} + b_{1} \\ 0 = 32k_{1} + b_{1}\end{cases}$,解得 $\begin{cases}k=\frac{2}{3} \\ b = -\frac{16}{3}\end{cases}$,$\begin{cases}k_{1}=-\frac{4}{3} \\ b_{1}=\frac{128}{3}\end{cases}$。
慢车离 A 站的路程 s 关于 t 的函数表达式为 $s=\frac{2}{3}t-\frac{16}{3}$,快车离 A 站的路程 s 关于 t 的函数表达式为 $s=-\frac{4}{3}t+\frac{128}{3}$,联立两式 $\begin{cases}s=\frac{2}{3}t-\frac{16}{3} \\ s=-\frac{4}{3}t+\frac{128}{3}\end{cases}$,解得 $\begin{cases}t = 24 \\ s=\frac{32}{3}\end{cases}$,即第一次相遇时与 A 站的距离为 $\frac{32}{3}km$。
(3) 由
(2),得 $t_{1}=12 + 8 + 4 = 24$,由题意可得函数图象关于过点 $(36,0)$ 且垂直于横轴的直线对称,$P_{1}$,$P_{2}$ 是一组对称点,所以 $t_{2}-36 = 36 - t_{1}$,解得 $t_{2}=48$,$t_{2}-t_{1}=24$。所以第一次相遇后,经过 24 min 后两车再次相遇。