1.
斜边
和一条直角边
分别相等的两个直角三角形全等,可以简写成“斜边、直角边”或“HL
”.答案:斜边,直角边,HL
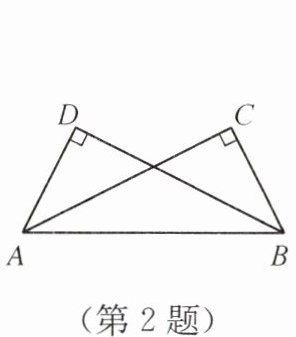
2. 如图,∠C= ∠D= 90°,请你再添加一个条件,使△ABD≌△BAC,并在添加的条件后的括号内写出判定全等的依据.
(1)
(3)
(1)
AD=BC
(HL
);(2)∠DAB=∠CBA
(AAS
);(3)
DB=CA
(HL
);(4)∠DBA=∠CAB
(AAS
).
答案:
(1) AD=BC(HL)
(2) ∠DAB=∠CBA(AAS)
(3) DB=CA(HL)
(4) ∠DBA=∠CAB(AAS)
(1) AD=BC(HL)
(2) ∠DAB=∠CBA(AAS)
(3) DB=CA(HL)
(4) ∠DBA=∠CAB(AAS)
3. 如图,用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是(
A.ASA
B.AAS
C.SAS
D.HL
A
)A.ASA
B.AAS
C.SAS
D.HL
答案:A
4. 如图,要用“HL”证明Rt△ABC≌Rt△ABD,则需要添加的一个条件是(
A.∠C= ∠D
B.AC= BD
C.BC= BD
D.AD= BC
C
)A.∠C= ∠D
B.AC= BD
C.BC= BD
D.AD= BC
答案:C
解析:
在Rt△ABC和Rt△ABD中,∠C=∠D=90°,AB为公共斜边。
要利用“HL”证明全等,需添加一组直角边相等。
选项中BC和BD为一组直角边,添加BC=BD,则有AB=AB,BC=BD,可证Rt△ABC≌Rt△ABD。
C
要利用“HL”证明全等,需添加一组直角边相等。
选项中BC和BD为一组直角边,添加BC=BD,则有AB=AB,BC=BD,可证Rt△ABC≌Rt△ABD。
C
5. 如图,BE⊥AC,CF⊥AB,垂足分别是E,F. 若BE= CF,则图中全等三角形有(

A.1对
B.2对
C.3对
D.4对
C
).
A.1对
B.2对
C.3对
D.4对
答案:C
解析:
在△ABE和△ACF中,∠AEB=∠AFC=90°,∠A=∠A,BE=CF,
∴△ABE≌△ACF(AAS),
∴AB=AC,AE=AF;
∵AB=AC,
∴∠ABC=∠ACB;
在△BFC和△CEB中,∠BFC=∠CEB=90°,∠FBC=∠ECB,BC=CB,
∴△BFC≌△CEB(AAS);
∵AE=AF,AB=AC,
∴BF=CE;
在△BOF和△COE中,∠BFO=∠CEO=90°,∠BOF=∠COE,BF=CE,
∴△BOF≌△COE(AAS);
共3对全等三角形。C
∴△ABE≌△ACF(AAS),
∴AB=AC,AE=AF;
∵AB=AC,
∴∠ABC=∠ACB;
在△BFC和△CEB中,∠BFC=∠CEB=90°,∠FBC=∠ECB,BC=CB,
∴△BFC≌△CEB(AAS);
∵AE=AF,AB=AC,
∴BF=CE;
在△BOF和△COE中,∠BFO=∠CEO=90°,∠BOF=∠COE,BF=CE,
∴△BOF≌△COE(AAS);
共3对全等三角形。C
6. 如图,在正方形网格中,A,B,C,D均为格点,则∠ACD+∠BDC= ______°.


90
答案:90
解析:
连接AD,设每个小正方形边长为1。
由勾股定理得:
$AC=\sqrt{1^2 + 2^2}=\sqrt{5}$,
$CD=\sqrt{2^2 + 2^2}=2\sqrt{2}$,
$AD=\sqrt{1^2 + 3^2}=\sqrt{10}$,
$BD=\sqrt{1^2 + 1^2}=\sqrt{2}$,
$BC=\sqrt{1^2 + 1^2}=\sqrt{2}$。
在$\triangle ACD$中,$AC^2 + AD^2 = (\sqrt{5})^2 + (\sqrt{10})^2 = 5 + 10 = 15$,$CD^2=(2\sqrt{2})^2=8$,不满足勾股定理。
在$\triangle BCD$中,$BC=BD=\sqrt{2}$,$CD=2\sqrt{2}$,则$BC^2 + BD^2 = (\sqrt{2})^2 + (\sqrt{2})^2 = 2 + 2 = 4$,$CD^2=(2\sqrt{2})^2=8$,不满足勾股定理。
延长CD至点E,使DE=BC=\sqrt{2},连接BE。
$\angle BDE = \angle BDC$(对顶角相等),$DE=BC$,$BD=BD$,故$\triangle BDE \cong \triangle BDC$(SAS),则$\angle BED = \angle BCD$。
在$\triangle ACE$中,$AC=\sqrt{5}$,$CE=CD + DE=2\sqrt{2} + \sqrt{2}=3\sqrt{2}$,$AE=\sqrt{(1 + 1)^2 + (3 - 1)^2}=\sqrt{4 + 4}=2\sqrt{2}$。
$AC^2 + AE^2 = (\sqrt{5})^2 + (2\sqrt{2})^2 = 5 + 8 = 13$,$CE^2=(3\sqrt{2})^2=18$,不满足勾股定理。
另取格点F(坐标设为(3,2)),连接CF、DF。
$CF=\sqrt{(3 - 2)^2 + (2 - 3)^2}=\sqrt{1 + 1}=\sqrt{2}$,$DF=\sqrt{(3 - 4)^2 + (2 - 1)^2}=\sqrt{1 + 1}=\sqrt{2}$,$CD=2\sqrt{2}$,则$\triangle CDF$为等腰直角三角形,$\angle CFD=90^\circ$,$\angle FCD=45^\circ$。
$\angle ACD + \angle FCD = \angle ACF$,$\angle ACF + \angle BDC = 45^\circ + 45^\circ = 90^\circ$。
90
由勾股定理得:
$AC=\sqrt{1^2 + 2^2}=\sqrt{5}$,
$CD=\sqrt{2^2 + 2^2}=2\sqrt{2}$,
$AD=\sqrt{1^2 + 3^2}=\sqrt{10}$,
$BD=\sqrt{1^2 + 1^2}=\sqrt{2}$,
$BC=\sqrt{1^2 + 1^2}=\sqrt{2}$。
在$\triangle ACD$中,$AC^2 + AD^2 = (\sqrt{5})^2 + (\sqrt{10})^2 = 5 + 10 = 15$,$CD^2=(2\sqrt{2})^2=8$,不满足勾股定理。
在$\triangle BCD$中,$BC=BD=\sqrt{2}$,$CD=2\sqrt{2}$,则$BC^2 + BD^2 = (\sqrt{2})^2 + (\sqrt{2})^2 = 2 + 2 = 4$,$CD^2=(2\sqrt{2})^2=8$,不满足勾股定理。
延长CD至点E,使DE=BC=\sqrt{2},连接BE。
$\angle BDE = \angle BDC$(对顶角相等),$DE=BC$,$BD=BD$,故$\triangle BDE \cong \triangle BDC$(SAS),则$\angle BED = \angle BCD$。
在$\triangle ACE$中,$AC=\sqrt{5}$,$CE=CD + DE=2\sqrt{2} + \sqrt{2}=3\sqrt{2}$,$AE=\sqrt{(1 + 1)^2 + (3 - 1)^2}=\sqrt{4 + 4}=2\sqrt{2}$。
$AC^2 + AE^2 = (\sqrt{5})^2 + (2\sqrt{2})^2 = 5 + 8 = 13$,$CE^2=(3\sqrt{2})^2=18$,不满足勾股定理。
另取格点F(坐标设为(3,2)),连接CF、DF。
$CF=\sqrt{(3 - 2)^2 + (2 - 3)^2}=\sqrt{1 + 1}=\sqrt{2}$,$DF=\sqrt{(3 - 4)^2 + (2 - 1)^2}=\sqrt{1 + 1}=\sqrt{2}$,$CD=2\sqrt{2}$,则$\triangle CDF$为等腰直角三角形,$\angle CFD=90^\circ$,$\angle FCD=45^\circ$。
$\angle ACD + \angle FCD = \angle ACF$,$\angle ACF + \angle BDC = 45^\circ + 45^\circ = 90^\circ$。
90