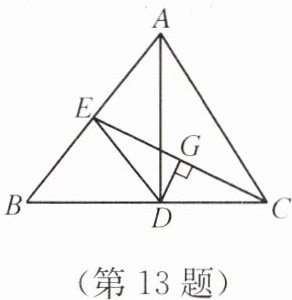
13. 如图,在△ABC中,AD是高,CE是中线,G是CE的中点,DG⊥CE,垂足为G,连接DE. 求证:DC=BE.

答案:因为点 G 是 CE 的中点,DG⊥CE,所以 DE=DC.又 CE 是中线,所以 AE=BE,又 AD 是高,故 DE=BE,所以 DC=BE.
解析:
证明:
∵G是CE的中点,DG⊥CE,
∴DG是CE的垂直平分线,
∴DE=DC。
∵CE是△ABC的中线,
∴E是AB的中点,即AE=BE。
∵AD是△ABC的高,
∴△ABD是直角三角形,DE是Rt△ABD斜边AB上的中线,
∴DE=BE。
∴DC=BE。
∵G是CE的中点,DG⊥CE,
∴DG是CE的垂直平分线,
∴DE=DC。
∵CE是△ABC的中线,
∴E是AB的中点,即AE=BE。
∵AD是△ABC的高,
∴△ABD是直角三角形,DE是Rt△ABD斜边AB上的中线,
∴DE=BE。
∴DC=BE。
14. 如图,在△ABC中,∠B=90°,AB=16 cm,BC=12 cm,AC=20 cm,P,Q是△ABC边上的两个动点,其中点P从点A开始按A→B的路径运动,且速度为1 cm/s,点Q从点B开始按B→C→A的路径运动,且速度为2 cm/s,它们同时出发,设出发的时间为t s.
(1)BP=
(2)当点Q在边BC上运动时,出发几秒后,△PQB是等腰三角形?
(3)当点Q在边CA上运动时,出发
(1)BP=
16 - t
(用含t的代数式表示)cm.(2)当点Q在边BC上运动时,出发几秒后,△PQB是等腰三角形?
当△PQB为等腰三角形时,有 BP=BQ,即 16 - t=2t,则 t=$\frac{16}{3}$
(3)当点Q在边CA上运动时,出发
11 或 12
s后,△BCQ是以BC或BQ为底边的等腰三角形.答案:
(1) 16 - t
(2) 当△PQB为等腰三角形时,有 BP=BQ,即 16 - t=2t,则 t=$\frac{16}{3}$
(3) 11 或 12
(1) 16 - t
(2) 当△PQB为等腰三角形时,有 BP=BQ,即 16 - t=2t,则 t=$\frac{16}{3}$
(3) 11 或 12