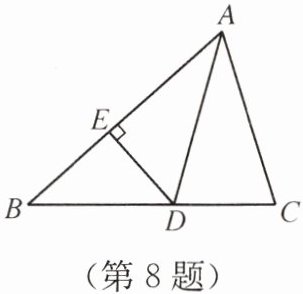
8. 如图,在△ABC中,AD平分∠BAC,DE⊥AB. 若AC= 2,DE= 1,则S△ACD= ______.

1
答案:1
解析:
过点D作DF⊥AC于点F。
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DF=DE=1。
∵AC=2,
∴S△ACD=$\frac{1}{2}×AC×DF=\frac{1}{2}×2×1=1$。
1
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DF=DE=1。
∵AC=2,
∴S△ACD=$\frac{1}{2}×AC×DF=\frac{1}{2}×2×1=1$。
1
9. 如图,在△ABC中,∠BAC= 108°,PM和QN分别是边AB和AC的垂直平分线,则∠PAQ=
36
°.答案:36
解析:
∵PM和QN分别是边AB和AC的垂直平分线,
∴PA=PB,QA=QC,
∴∠PAB=∠B,∠QAC=∠C,
∵∠BAC=108°,
∴∠B+∠C=180°-∠BAC=72°,
∴∠PAB+∠QAC=72°,
∴∠PAQ=∠BAC-(∠PAB+∠QAC)=108°-72°=36°
36
10. 如图,AD,AF分别是△ABC的中线和高,BE是△ABD的角平分线.
(1)若∠BED= 60°,∠BAD= 40°,求∠BAF的度数;
(2)若AB= 8,AC= 6,求中线AD的长的取值范围.

(1)若∠BED= 60°,∠BAD= 40°,求∠BAF的度数;
(2)若AB= 8,AC= 6,求中线AD的长的取值范围.

答案:
(1) 因为∠BED=∠ABE+∠BAE,∠BED=60°,∠BAD=40°,所以∠ABE=60°-40°=20°. 因为 BE 平分∠ABC,所以∠ABC=2∠ABE=40°. 因为 AF 为高,所以∠AFB=90°,所以∠BAF=90°-∠ABF=90°-40°=50°
(2) 延长 AD 至点 K,使 AD=DK,连接 CK. 因为 AD 是△ABC 的中线,所以 BD=CD. 又因为∠ADB=∠CDK,所以△ADB≌△KDC,所以 AB=CK=8,而 AC=6,故 2<AK<14,即 1<AD<7
(1) 因为∠BED=∠ABE+∠BAE,∠BED=60°,∠BAD=40°,所以∠ABE=60°-40°=20°. 因为 BE 平分∠ABC,所以∠ABC=2∠ABE=40°. 因为 AF 为高,所以∠AFB=90°,所以∠BAF=90°-∠ABF=90°-40°=50°
(2) 延长 AD 至点 K,使 AD=DK,连接 CK. 因为 AD 是△ABC 的中线,所以 BD=CD. 又因为∠ADB=∠CDK,所以△ADB≌△KDC,所以 AB=CK=8,而 AC=6,故 2<AK<14,即 1<AD<7
11. 如图,已知AB= AC,M,N分别是AC,AB的中点,连接BM,CN.
(1)求证:△ABM≌△ACN;
(2)求证:OB= OC.

(1)求证:△ABM≌△ACN;
(2)求证:OB= OC.

答案:
(1) 因为 M,N 分别为 AC,AB 的中点,所以 AM=AN=$\frac{1}{2}AB=\frac{1}{2}AC$. 又因为 AB=AC,∠A=∠A,所以△ABM≌△CAN
(2) 由
(1)知△ABM≌△CAN,所以∠B=∠C. 又因为 AB=AC,AM=AN,所以 CM=BN. 又∠MOC=∠NOB,所以△MOC≌△NOB,故 OB=OC
(1) 因为 M,N 分别为 AC,AB 的中点,所以 AM=AN=$\frac{1}{2}AB=\frac{1}{2}AC$. 又因为 AB=AC,∠A=∠A,所以△ABM≌△CAN
(2) 由
(1)知△ABM≌△CAN,所以∠B=∠C. 又因为 AB=AC,AM=AN,所以 CM=BN. 又∠MOC=∠NOB,所以△MOC≌△NOB,故 OB=OC