11. 求下列各式中$x$的值:
(1)$x^3= -64$;
(2)$8x^3-125= 0$;
(3)$(x-2)^3= -343$.
(1)$x^3= -64$;
(2)$8x^3-125= 0$;
(3)$(x-2)^3= -343$.
答案:
(1)$x=-4$
(2)$x=\frac{5}{2}$
(3)$x=-5$
(1)$x=-4$
(2)$x=\frac{5}{2}$
(3)$x=-5$
12. 已知$a+5$的算术平方根是2,$a+3b$的立方根是2.
(1)求$a$,$b$的值;
(2)求$a+b$的立方根.
(1)求$a$,$b$的值;
(2)求$a+b$的立方根.
答案:
(1)
∵$a + 5$的算术平方根是2,
∴$a + 5 = 4$,
∴$a = -1$.
∵$a + 3b$的立方根是2,
∴$a + 3b = 8$,
∴$-1 + 3b = 8$,
∴$b = 3$
(2)由
(1)知,$a = -1,b = 3$,
∴$a + b = -1 + 3 = 2$,
∴$a + b$的立方根是$\sqrt[3]{2}$
(1)
∵$a + 5$的算术平方根是2,
∴$a + 5 = 4$,
∴$a = -1$.
∵$a + 3b$的立方根是2,
∴$a + 3b = 8$,
∴$-1 + 3b = 8$,
∴$b = 3$
(2)由
(1)知,$a = -1,b = 3$,
∴$a + b = -1 + 3 = 2$,
∴$a + b$的立方根是$\sqrt[3]{2}$
13. 如图,有一张面积为$400\ cm^2$的正方形硬纸片.
(1)该正方形纸片的边长为______;(直接写出答案)
(2)若用此正方形纸片制作一个体积为$216\ cm^3$的无盖正方体纸盒,请在这张正方形纸片上画出无盖正方体的平面展开图的示意图,并求出该纸盒所用纸片的面积.

(1)该正方形纸片的边长为______;(直接写出答案)
(2)若用此正方形纸片制作一个体积为$216\ cm^3$的无盖正方体纸盒,请在这张正方形纸片上画出无盖正方体的平面展开图的示意图,并求出该纸盒所用纸片的面积.

答案:
(1)20cm
(2)因为无盖正方体的体积是$216\ cm^3$,所以边长为6cm.无盖正方体的展示图如图所示,所用面积为$5×6^2 = 180(cm^2)$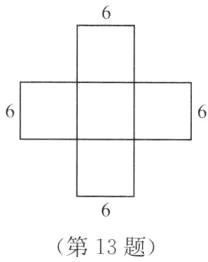
(1)20cm
(2)因为无盖正方体的体积是$216\ cm^3$,所以边长为6cm.无盖正方体的展示图如图所示,所用面积为$5×6^2 = 180(cm^2)$

14. 仿照平方根、立方根的定义,我们可以定义$n$次方根如下:如果一个数的$n$次方($n$是大于1的整数)等于$a$,那么这个数叫作$a的n$次方根,$a的正的n次方根记作\sqrt[n]{a}$,负的$n次方根记作-\sqrt[n]{a}$.
(1)求-1024的5次方根、1024的10次方根;
(2)求$\sqrt[4]{16}$,$\sqrt[5]{-243}$;
(3)已知$a>0$,$n$为正整数,求$a的n$次方根.
(1)求-1024的5次方根、1024的10次方根;
(2)求$\sqrt[4]{16}$,$\sqrt[5]{-243}$;
(3)已知$a>0$,$n$为正整数,求$a的n$次方根.
答案:
(1)-1024的5次方根是-4,1024的10次方根是$\pm2$
(2)$\sqrt[4]{16}=2$,$\sqrt[5]{-243}=-3$
(3)当n是正偶数时,a的n次方根是$\pm\sqrt[n]{a}$;当n是正奇数时,a的n次方根是$\sqrt[n]{a}$
(1)-1024的5次方根是-4,1024的10次方根是$\pm2$
(2)$\sqrt[4]{16}=2$,$\sqrt[5]{-243}=-3$
(3)当n是正偶数时,a的n次方根是$\pm\sqrt[n]{a}$;当n是正奇数时,a的n次方根是$\sqrt[n]{a}$