11. 写出所有大于$-\sqrt{5}且小于\sqrt{17}$的整数.
答案:-2,-1,0,1,2,3,4
12. 如图是一个无理数筛选器的工作流程图.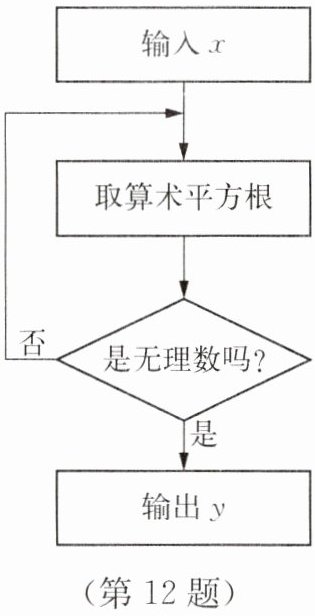
(1)当$x$为9时,求$y$的值;
(2)如果输入0或1,那么______(填“能”或“不能”)输出$y$值;
(3)当输出的$y的值是\sqrt{5}$时,请写出满足题意的$x$值:______.(写出两个即可)
(1)
(2)
(3)

(1)当$x$为9时,求$y$的值;
(2)如果输入0或1,那么______(填“能”或“不能”)输出$y$值;
(3)当输出的$y的值是\sqrt{5}$时,请写出满足题意的$x$值:______.(写出两个即可)
(1)
$\sqrt{3}$
(2)
不能
(3)
5,25
答案:
(1)当输入$x=9$时,9的算术平方根为3,不是无理数,3的算术平方根为$\sqrt{3}$,即$y=$$\sqrt{3}$
(2)不能
(3)当$y=\sqrt{5}$时,$y^{2}=(\sqrt{5})^{2}=5$,此时$x=5$;当$y=\sqrt{5}$时,$y^{2}=(\sqrt{5})^{2}=5$,$5^{2}=25$,此时$x=25$(答案不唯一)
(1)当输入$x=9$时,9的算术平方根为3,不是无理数,3的算术平方根为$\sqrt{3}$,即$y=$$\sqrt{3}$
(2)不能
(3)当$y=\sqrt{5}$时,$y^{2}=(\sqrt{5})^{2}=5$,此时$x=5$;当$y=\sqrt{5}$时,$y^{2}=(\sqrt{5})^{2}=5$,$5^{2}=25$,此时$x=25$(答案不唯一)
13. 给定一个无理数$x$,对于任意有理数$a$,$b$,如果$ax + b = 0$,那么$a = b = 0$. 这种说法正确吗?说明理由.(提示:可以使用反证法)
答案:假设$a\neq 0$,则$ax=-b$,$x=-\frac{b}{a}$,$x$为有理数,与$x$为无理数矛盾.所以$a=0$,从而$b=0$.故结论正确
解析:
这种说法正确。
证明:假设$a \neq 0$,则由$ax + b = 0$可得$ax=-b$,进而$x=-\frac{b}{a}$。
因为$a$,$b$为有理数,所以$-\frac{b}{a}$为有理数,这与$x$是无理数矛盾,故假设不成立,所以$a = 0$。
将$a = 0$代入$ax + b = 0$,得$0 \cdot x + b = 0$,即$b = 0$。
综上,$a = b = 0$。
证明:假设$a \neq 0$,则由$ax + b = 0$可得$ax=-b$,进而$x=-\frac{b}{a}$。
因为$a$,$b$为有理数,所以$-\frac{b}{a}$为有理数,这与$x$是无理数矛盾,故假设不成立,所以$a = 0$。
将$a = 0$代入$ax + b = 0$,得$0 \cdot x + b = 0$,即$b = 0$。
综上,$a = b = 0$。