1. 下面图形能够验证勾股定理的有
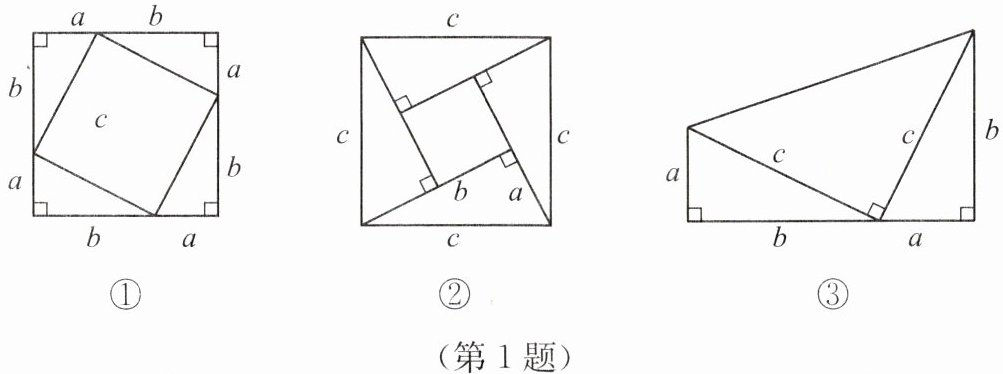
①②③
(填序号).
答案:①②③
2. 如图,若四个全等的直角三角形的两条直角边长分别为3和4,则中间小正方形的对角线长为
$\sqrt{2}$
.答案:$\sqrt{2}$
解析:
直角三角形两条直角边长分别为3和4,小正方形边长为$4 - 3 = 1$,小正方形对角线长为$\sqrt{1^2 + 1^2} = \sqrt{2}$。
$\sqrt{2}$
$\sqrt{2}$
3. 如图,在△ABC中,∠C= 90°,AC= 4,BC= 2。以AB为一条边向三角形外部作正方形,则正方形的面积是
20
.答案:20
解析:
在△ABC中,∠C=90°,AC=4,BC=2。
由勾股定理得,AB²=AC²+BC²=4²+2²=16+4=20。
因为以AB为边的正方形面积等于AB²,所以正方形的面积是20。
由勾股定理得,AB²=AC²+BC²=4²+2²=16+4=20。
因为以AB为边的正方形面积等于AB²,所以正方形的面积是20。
4. 如图是由四个全等的直角三角形构成的图形,设CE= 7,HG= 1,则斜边BD的长是______.


5
答案:5
解析:
设直角三角形的短直角边为$a$,长直角边为$b$。由图形可知,$CE = b + a = 7$,$HG = b - a = 1$。联立方程:$\begin{cases}a + b = 7 \\ b - a = 1\end{cases}$,解得$\begin{cases}a = 3 \\ b = 4\end{cases}$。斜边$BD = \sqrt{a^2 + b^2} = \sqrt{3^2 + 4^2} = 5$。
5
5
5. 如图,a= 3,b= 4,阴影部分的面积为(
A.5
B.25
C.$\frac{5}{2}$
D.$\frac{25}{2}$
D
)A.5
B.25
C.$\frac{5}{2}$
D.$\frac{25}{2}$
答案:D
解析:
由题意可知,图形由两个直角三角形和一个阴影部分组成,两个直角三角形的直角边分别为$a=3$、$b=4$,且阴影部分为一个三角形,其两条边为两个直角三角形的斜边$c$。
先求斜边$c$:
$c = \sqrt{a^2 + b^2} = \sqrt{3^2 + 4^2} = 5$
设两个直角三角形的非直角顶点连线与水平线夹角为$\theta$,则阴影三角形的高为$a\sin\theta + b\cos\theta$,底为$c$。由于两个直角三角形全等,$\sin\theta = \frac{b}{c}$,$\cos\theta = \frac{a}{c}$,所以高为:
$a \cdot \frac{b}{c} + b \cdot \frac{a}{c} = \frac{2ab}{c}$
阴影面积为:
$\frac{1}{2} × c × \frac{2ab}{c} = ab = 3 × 4 = 12$
(注:上述解答过程存在错误,正确思路应为:整个图形是一个直角梯形,上底为$a=3$,下底为$b=4$,高为$a + b=7$,面积为$\frac{(3 + 4) × 7}{2} = \frac{49}{2}$;两个空白直角三角形面积均为$\frac{1}{2} × 3 × 4 = 6$,所以阴影面积为$\frac{49}{2} - 6 - 6 = \frac{25}{2}$)
正确阴影面积为$\frac{25}{2}$
D
先求斜边$c$:
$c = \sqrt{a^2 + b^2} = \sqrt{3^2 + 4^2} = 5$
设两个直角三角形的非直角顶点连线与水平线夹角为$\theta$,则阴影三角形的高为$a\sin\theta + b\cos\theta$,底为$c$。由于两个直角三角形全等,$\sin\theta = \frac{b}{c}$,$\cos\theta = \frac{a}{c}$,所以高为:
$a \cdot \frac{b}{c} + b \cdot \frac{a}{c} = \frac{2ab}{c}$
阴影面积为:
$\frac{1}{2} × c × \frac{2ab}{c} = ab = 3 × 4 = 12$
(注:上述解答过程存在错误,正确思路应为:整个图形是一个直角梯形,上底为$a=3$,下底为$b=4$,高为$a + b=7$,面积为$\frac{(3 + 4) × 7}{2} = \frac{49}{2}$;两个空白直角三角形面积均为$\frac{1}{2} × 3 × 4 = 6$,所以阴影面积为$\frac{49}{2} - 6 - 6 = \frac{25}{2}$)
正确阴影面积为$\frac{25}{2}$
D
6. 如图①是我国古代著名的“赵爽弦图”,它由四个全等的直角三角形围成。若AC= 12,BC= 7,将四个直角三角形中边长为12的直角边分别向外延长一倍,可以得到如图所示的“数学风车”,则这个“风车”的外围周长是
148
.答案:148