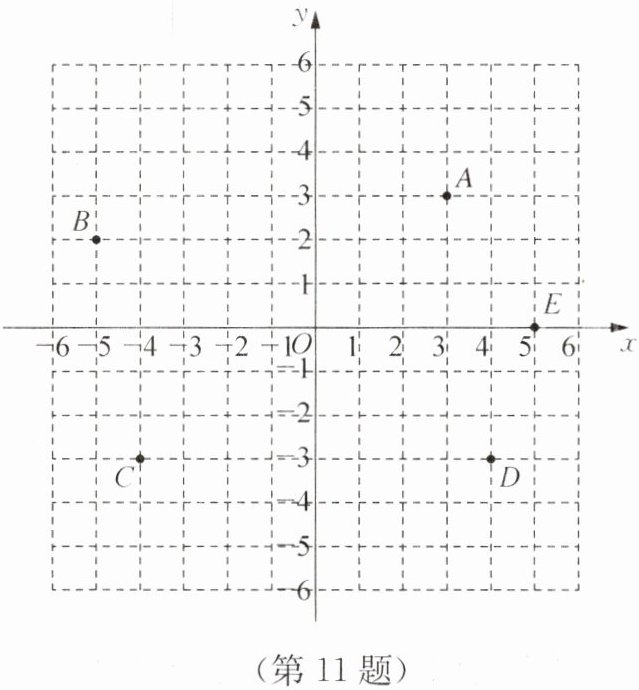
11. 如图,在平面直角坐标系中有A,B,C,D,E,完成问题:
(1)写出点A,B,C,D,E的坐标.
(2)将点A,B,C,D,E的横坐标、纵坐标分别乘-1,得到点A',B',C',D',E',描出各点.
(3)求四边形ABCD和四边形A'B'C'D'的面积.
(1)写出点A,B,C,D,E的坐标.
(2)将点A,B,C,D,E的横坐标、纵坐标分别乘-1,得到点A',B',C',D',E',描出各点.
(3)求四边形ABCD和四边形A'B'C'D'的面积.

答案:
(1) A(3,3),B(-5,2),C(-4,-3),D(4,-3),E(5,0)
(2) 图略
(3) 用割补法,$S=9×6-\frac {5}{2}-\frac {6}{2}-\frac {8}{2}=\frac {99}{2}$
(1) A(3,3),B(-5,2),C(-4,-3),D(4,-3),E(5,0)
(2) 图略
(3) 用割补法,$S=9×6-\frac {5}{2}-\frac {6}{2}-\frac {8}{2}=\frac {99}{2}$
12. 如图,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足$|a+1|+\sqrt{b-5}= 0$,点C的坐标为(0,3).
(1)求点A,B的坐标;
(2)若P为y轴上的一点,且△PBC的面积为15,求点P的坐标.

(1)求点A,B的坐标;
(2)若P为y轴上的一点,且△PBC的面积为15,求点P的坐标.

答案:1. (1)
因为$\vert a + 1\vert+\sqrt{b - 5}=0$,
又因为$\vert a + 1\vert\geq0$,$\sqrt{b - 5}\geq0$,
根据非负数的性质:若$m + n=0$($m\geq0$,$n\geq0$),则$m = 0$且$n = 0$,
所以$a+1 = 0$,解得$a=-1$;$b - 5=0$,解得$b = 5$。
则点$A$的坐标为$(-1,0)$,点$B$的坐标为$(5,0)$。
2. (2)
设点$P$的坐标为$(0,y)$。
已知$B(5,0)$,$C(0,3)$,根据三角形面积公式$S=\frac{1}{2}×底×高$,对于$\triangle PBC$,以$BC$为底时,底$\vert BC\vert=\vert y - 3\vert$,高为点$B$到$y$轴的距离,即高$h = 5$。
由$S_{\triangle PBC}=15$,根据$S=\frac{1}{2}×\vert BC\vert×5$,可得$\frac{1}{2}×\vert y - 3\vert×5 = 15$。
先化简方程:
$\vert y - 3\vert×5=30$,则$\vert y - 3\vert=6$。
再根据绝对值的定义求解:
当$y-3 = 6$时,$y=6 + 3=9$;
当$y - 3=-6$时,$y=-6 + 3=-3$。
所以点$P$的坐标为$(0,9)$或$(0,-3)$。
因为$\vert a + 1\vert+\sqrt{b - 5}=0$,
又因为$\vert a + 1\vert\geq0$,$\sqrt{b - 5}\geq0$,
根据非负数的性质:若$m + n=0$($m\geq0$,$n\geq0$),则$m = 0$且$n = 0$,
所以$a+1 = 0$,解得$a=-1$;$b - 5=0$,解得$b = 5$。
则点$A$的坐标为$(-1,0)$,点$B$的坐标为$(5,0)$。
2. (2)
设点$P$的坐标为$(0,y)$。
已知$B(5,0)$,$C(0,3)$,根据三角形面积公式$S=\frac{1}{2}×底×高$,对于$\triangle PBC$,以$BC$为底时,底$\vert BC\vert=\vert y - 3\vert$,高为点$B$到$y$轴的距离,即高$h = 5$。
由$S_{\triangle PBC}=15$,根据$S=\frac{1}{2}×\vert BC\vert×5$,可得$\frac{1}{2}×\vert y - 3\vert×5 = 15$。
先化简方程:
$\vert y - 3\vert×5=30$,则$\vert y - 3\vert=6$。
再根据绝对值的定义求解:
当$y-3 = 6$时,$y=6 + 3=9$;
当$y - 3=-6$时,$y=-6 + 3=-3$。
所以点$P$的坐标为$(0,9)$或$(0,-3)$。