7. 已知等边三角形ABC的边长为2,以BC的中点为原点,BC所在的直线为x轴建立平面直角坐标系,则点A的坐标为
(0,$\sqrt{3}$)或(0,$-\sqrt{3}$)
.答案:(0,$\sqrt{3}$)或(0,$-\sqrt{3}$)
解析:
因为等边三角形ABC的边长为2,以BC的中点为原点,BC所在直线为x轴建立平面直角坐标系,所以BC=2,BO=OC=1。在Rt△ABO中,AB=2,BO=1,根据勾股定理可得AO=$\sqrt{AB^{2}-BO^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$。由于点A可能在x轴上方或下方,所以点A的坐标为(0,$\sqrt{3}$)或(0,$-\sqrt{3}$)。
(0,$\sqrt{3}$)或(0,$-\sqrt{3}$)
(0,$\sqrt{3}$)或(0,$-\sqrt{3}$)
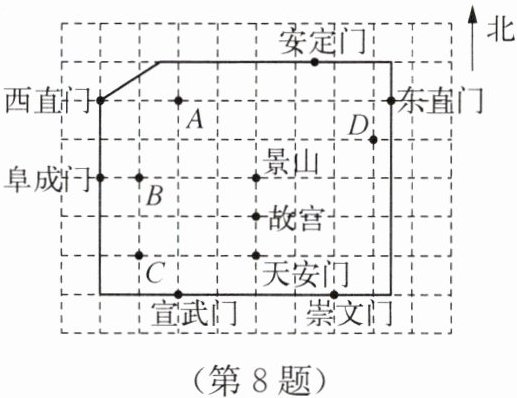
8. 如图是老北京城的一些地点分布示意图,已知东直门和宣武门的坐标分别为(3.5,4),(-2,-1).
(1) 在图中画出相应的平面直角坐标系,并写出(-4,2)表示的地点;
(2) 根据(1)中建立的平面直角坐标系,写出示意图中西直门和崇文门的坐标;
(3) 根据(1)中建立的平面直角坐标系,李华计划骑一辆共享单车,已知单车在A,B,C,D四处,李华在安定门,请直接写出距离李华最近的共享单车的位置坐标.
(1) 在图中画出相应的平面直角坐标系,并写出(-4,2)表示的地点;
(2) 根据(1)中建立的平面直角坐标系,写出示意图中西直门和崇文门的坐标;
(3) 根据(1)中建立的平面直角坐标系,李华计划骑一辆共享单车,已知单车在A,B,C,D四处,李华在安定门,请直接写出距离李华最近的共享单车的位置坐标.

答案:
(1) 平面直角坐标系如图,(-4,2)表示的点是阜成门
(2) 西直门的坐标是(-4,4),崇文门的坐标是(2,-1)
(3) 最近的共享单车在(3,3)
(1) 平面直角坐标系如图,(-4,2)表示的点是阜成门

(2) 西直门的坐标是(-4,4),崇文门的坐标是(2,-1)
(3) 最近的共享单车在(3,3)
9. 如图,已知在长方形OABC中,AB//OC,AO//BC,O为平面直角坐标系的原点,OA= 8,OC= 4,点B在第一象限.
(1) 直接写出点B的坐标:
(2) 若点P从点C出发沿CB方向匀速移动(不超过点B),点Q从点B出发沿BA方向匀速运动(不超过点A),且点Q的速度是点P的一半,已知P,Q两点同时出发,设点P的坐标为(m,4),试表示四边形PBQO的面积.

(1) 直接写出点B的坐标:
(8,4)
.(2) 若点P从点C出发沿CB方向匀速移动(不超过点B),点Q从点B出发沿BA方向匀速运动(不超过点A),且点Q的速度是点P的一半,已知P,Q两点同时出发,设点P的坐标为(m,4),试表示四边形PBQO的面积.
设点 Q 的运动速度为 v,运动时间为 t,则点 P 的运动速度为 2v,运动时间为$\frac{t}{2}$.设 CP=m,则 AQ=4 - 0.5m,∴$S_{四边形PBQO}=8×4-\frac{1}{2}×4×m-\frac{1}{2}×8×(4 - 0.5m)=16$,∴四边形 PBQO 的面积为 16

答案:
(1)(8,4)
(2)设点 Q 的运动速度为 v,运动时间为 t,则点 P 的运动速度为 2v,运动时间为$\frac{t}{2}$.设 CP=m,则 AQ=4 - 0.5m,
∴$S_{四边形PBQO}=8×4-\frac{1}{2}×4×m-\frac{1}{2}×8×(4 - 0.5m)=16$,
∴四边形 PBQO 的面积为 16
(1)(8,4)
(2)设点 Q 的运动速度为 v,运动时间为 t,则点 P 的运动速度为 2v,运动时间为$\frac{t}{2}$.设 CP=m,则 AQ=4 - 0.5m,
∴$S_{四边形PBQO}=8×4-\frac{1}{2}×4×m-\frac{1}{2}×8×(4 - 0.5m)=16$,
∴四边形 PBQO 的面积为 16