11. 在同一平面直角坐标系中,画出函数$y= \frac{1}{5}x$,$y= x$,$y= 5x$的图象.

答案:
列表如下,图象如图
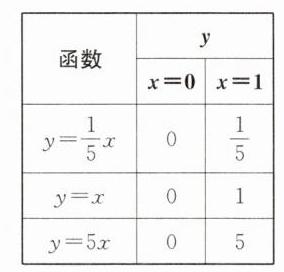

列表如下,图象如图


12. 定义运算“※”:$a※b= \begin{cases} ab(b\geq0), \\ -ab(b<0). \end{cases} $
(1)计算:3※4;
(2)画出函数$y= 2※x$的图象.

(1)计算:3※4;
(2)画出函数$y= 2※x$的图象.

答案:
(1)
∵4≥0,
∴3※4=3×4=12
(2)当x≥0时,y与x的关系式为y=2x;当x<0时,y与x的关系式为y=-2x;图象如图所示

(1)
∵4≥0,
∴3※4=3×4=12
(2)当x≥0时,y与x的关系式为y=2x;当x<0时,y与x的关系式为y=-2x;图象如图所示

13. 已知函数$y= x+\frac{1}{x}+1(x>0)$,仿照研究正比例函数图象的过程,完成表格,并根据表格中的数据,在平面直角坐标系中描点,画出函数$y= x+\frac{1}{x}+1(x>0)$的大致图象. 根据图象回答问题:观察正比例函数$y_1= 3x(x\geq0)$的图象,当x取何值时$y_1>y$?
| x | ... | $\frac{1}{4}$ | $\frac{1}{2}$ | 1 | 2 | 4 | ... |


| :--- | :--- | :------------ | :------------ | :--- | :--- | :--- | :--- |
| y | ... | ______ | ______ | 3 | ______ | ______ | ... |
| x | ... | $\frac{1}{4}$ | $\frac{1}{2}$ | 1 | 2 | 4 | ... |


| :--- | :--- | :------------ | :------------ | :--- | :--- | :--- | :--- |
| y | ... | ______ | ______ | 3 | ______ | ______ | ... |
答案:
完成表格如下,大致图象如图所示(合理即可),根据图象可得:当x>1时,$ y_{1}>y $
x ... $ \dfrac{1}{4} $ $ \dfrac{1}{2} $ 1 2 4 ...
y ... $ \dfrac{21}{4} $ $ \dfrac{7}{2} $ 3 $ \dfrac{7}{2} $ $ \dfrac{21}{4} $ ...

完成表格如下,大致图象如图所示(合理即可),根据图象可得:当x>1时,$ y_{1}>y $
x ... $ \dfrac{1}{4} $ $ \dfrac{1}{2} $ 1 2 4 ...
y ... $ \dfrac{21}{4} $ $ \dfrac{7}{2} $ 3 $ \dfrac{7}{2} $ $ \dfrac{21}{4} $ ...
