8. 用绘图软件绘制出函数$y= \frac{ax}{(x+b)^2}$的图象如图所示,根据你学习函数图象的经验,下列对$a$,$b$大小的判断,正确的是(
A.$a>0$,$b<0$
B.$a>0$,$b>0$
C.$a<0$,$b>0$
D.$a<0$,$b<0$
C
)A.$a>0$,$b<0$
B.$a>0$,$b>0$
C.$a<0$,$b>0$
D.$a<0$,$b<0$
答案:C
解析:
由函数$y=\frac{ax}{(x+b)^2}$的图象可知:
1. 当$x=0$时,$y=0$,函数过原点。
2. 当$x>0$时,$y<0$,此时$(x+b)^2>0$,则$ax<0$,又$x>0$,故$a<0$。
3. 函数定义域为$x\neq -b$,由图象知函数在$x=0$附近连续,无间断点,且当$x$趋近于$-b$时,分母趋近于0,函数值趋近于无穷。观察图象,左侧有渐近线在$y$轴左侧,即$-b<0$,所以$b>0$。
综上,$a<0$,$b>0$,答案选C。
1. 当$x=0$时,$y=0$,函数过原点。
2. 当$x>0$时,$y<0$,此时$(x+b)^2>0$,则$ax<0$,又$x>0$,故$a<0$。
3. 函数定义域为$x\neq -b$,由图象知函数在$x=0$附近连续,无间断点,且当$x$趋近于$-b$时,分母趋近于0,函数值趋近于无穷。观察图象,左侧有渐近线在$y$轴左侧,即$-b<0$,所以$b>0$。
综上,$a<0$,$b>0$,答案选C。
9. 若一个正比例函数的图象经过$A(m,6)$,$B(5,n)$两点,则$m$,$n$满足的关系式为______
mn=30
.答案:mn=30
解析:
设正比例函数的解析式为$y=kx(k\neq0)$。
因为函数图象经过$A(m,6)$,所以$6=km$,即$k=\dfrac{6}{m}(m\neq0)$。
又因为函数图象经过$B(5,n)$,所以$n=5k$,即$k=\dfrac{n}{5}(n\neq0)$。
则$\dfrac{6}{m}=\dfrac{n}{5}$,交叉相乘可得$mn=30$。
$mn=30$
因为函数图象经过$A(m,6)$,所以$6=km$,即$k=\dfrac{6}{m}(m\neq0)$。
又因为函数图象经过$B(5,n)$,所以$n=5k$,即$k=\dfrac{n}{5}(n\neq0)$。
则$\dfrac{6}{m}=\dfrac{n}{5}$,交叉相乘可得$mn=30$。
$mn=30$
10. 已知$y-2与3x-4$成正比例,且$x= 2$时,$y= 3$.
(1)求$y与x$之间的函数表达式;
(2)若点$(a,-3)$在这个函数的图象上,求$a$的值;
(3)若$y的取值范围是-1≤y≤1$,求$x$的取值范围.
(1)求$y与x$之间的函数表达式;
(2)若点$(a,-3)$在这个函数的图象上,求$a$的值;
(3)若$y的取值范围是-1≤y≤1$,求$x$的取值范围.
答案:
(1)y=$\frac{3}{2}$x
(2)a=-2
(3)-$\frac{2}{3}$≤x≤$\frac{2}{3}$
(1)y=$\frac{3}{2}$x
(2)a=-2
(3)-$\frac{2}{3}$≤x≤$\frac{2}{3}$
11. 已知函数$y= 2x$,$y= -2x$,$y= \frac{1}{2}x$,$y= -\frac{1}{2}x$.
(1)在图①的平面直角坐标系内画出各函数的图象.
(2)观察这些函数的图象,函数图象与$y轴的位置关系与|k|$有何关系?
(3)三个正比例函数的表达式分别为①$y= ax$,②$y= bx$,③$y= cx$,其在平面直角坐标系中的图象如图②所示,则$a$,$b$,$c$的大小关系为______
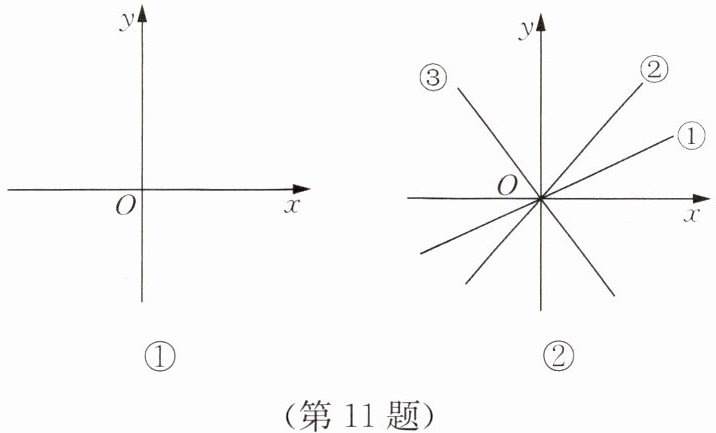
(1)在图①的平面直角坐标系内画出各函数的图象.
(2)观察这些函数的图象,函数图象与$y轴的位置关系与|k|$有何关系?
(3)三个正比例函数的表达式分别为①$y= ax$,②$y= bx$,③$y= cx$,其在平面直角坐标系中的图象如图②所示,则$a$,$b$,$c$的大小关系为______
b>a>c
.
答案:
(1)
(2)略
(3)b>a>c
(1)
(2)略
(3)b>a>c