1. 一般地,一次函数$y= kx+b的图象可以由正比例函数y= kx$的图象沿
y轴
向上$(b>0)或向下(b<0)$平移|b|
个单位长度得到. 画一次函数的图象只要确定图象上的两
个点即可.答案:y轴,|b|,两
2. 对于一次函数$y= x+2$,下列说法正确的是(
A.图象经过点$(2,0)$
B.图象不经过第三象限
C.图象与正比例函数$y= 2x$的图象平行
D.图象可由正比例函数$y= x$向上平移2个单位长度得到
D
)A.图象经过点$(2,0)$
B.图象不经过第三象限
C.图象与正比例函数$y= 2x$的图象平行
D.图象可由正比例函数$y= x$向上平移2个单位长度得到
答案:D
解析:
A. 当$x=2$时,$y=2+2=4$,图象经过点$(2,4)$,A错误;
B. 一次函数$y=x+2$,$k=1>0$,$b=2>0$,图象经过第一、二、三象限,B错误;
C. 正比例函数$y=2x$的斜率为$2$,一次函数$y=x+2$的斜率为$1$,$1\neq2$,两图象不平行,C错误;
D. 正比例函数$y=x$向上平移$2$个单位长度得到$y=x+2$,D正确。
结论:D
B. 一次函数$y=x+2$,$k=1>0$,$b=2>0$,图象经过第一、二、三象限,B错误;
C. 正比例函数$y=2x$的斜率为$2$,一次函数$y=x+2$的斜率为$1$,$1\neq2$,两图象不平行,C错误;
D. 正比例函数$y=x$向上平移$2$个单位长度得到$y=x+2$,D正确。
结论:D
3. 如图,某一次函数的图象与$x$轴、$y轴分别相交于(1,0)和(0,2)$两点,下列说法错误的是(
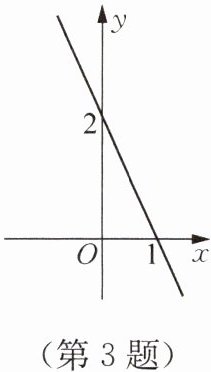
A.此函数的表达式为$y= -2x+2$
B.当$x>1$时,$y<0$
C.当$x<0$时,$y随x$的增大而增大
D.将此图象向下平移2个单位长度所得到的直线必过原点
C
)
A.此函数的表达式为$y= -2x+2$
B.当$x>1$时,$y<0$
C.当$x<0$时,$y随x$的增大而增大
D.将此图象向下平移2个单位长度所得到的直线必过原点
答案:C
解析:
设一次函数表达式为$y=kx+b$,将$(1,0)$,$(0,2)$代入得:
$\begin{cases}k+b=0\\b=2\end{cases}$,解得$k=-2$,$b=2$,函数表达式为$y=-2x+2$,A正确;
当$x>1$时,$y=-2x+2<-2×1 + 2=0$,B正确;
$k=-2<0$,$y$随$x$的增大而减小,C错误;
向下平移2个单位长度得$y=-2x+2 - 2=-2x$,过原点,D正确。
答案:C
$\begin{cases}k+b=0\\b=2\end{cases}$,解得$k=-2$,$b=2$,函数表达式为$y=-2x+2$,A正确;
当$x>1$时,$y=-2x+2<-2×1 + 2=0$,B正确;
$k=-2<0$,$y$随$x$的增大而减小,C错误;
向下平移2个单位长度得$y=-2x+2 - 2=-2x$,过原点,D正确。
答案:C
4. 将正比例函数$y= 2x$的图象向上平移3个单位长度后经过点$(1,m)$,则$m$的值为
5
.答案:5
解析:
将正比例函数$y = 2x$的图象向上平移3个单位长度,根据函数图象平移规律“上加下减”,得到的函数解析式为$y = 2x + 3$。
因为平移后的函数图象经过点$(1,m)$,将$x = 1$代入$y = 2x + 3$,可得$m = 2×1 + 3 = 5$。
5
因为平移后的函数图象经过点$(1,m)$,将$x = 1$代入$y = 2x + 3$,可得$m = 2×1 + 3 = 5$。
5
5. 一次函数$y= -2x+5的图象与y$轴的交点的坐标是
(0,5)
.答案:(0,5)
6. 在平面直角坐标系中,将正比例函数$y= kx(k>0)$的图象向右平移1个单位长度,则平移后的图象不经过(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
B
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:B
解析:
将正比例函数$y = kx(k>0)$的图象向右平移1个单位长度,根据函数图象平移规律“左加右减”,平移后的函数解析式为$y = k(x - 1)=kx - k$。
因为$k>0$,所以一次函数$y = kx - k$的斜率$k>0$,截距$-k<0$。
斜率大于0,函数图象从左到右上升;截距小于0,函数图象与$y$轴交于负半轴。
所以平移后的图象经过第一、三、四象限,不经过第二象限。
B
因为$k>0$,所以一次函数$y = kx - k$的斜率$k>0$,截距$-k<0$。
斜率大于0,函数图象从左到右上升;截距小于0,函数图象与$y$轴交于负半轴。
所以平移后的图象经过第一、三、四象限,不经过第二象限。
B
7. 将正比例函数$y= kx$的图象向右平移2个单位长度,再向下平移4个单位长度,平移后的图象经过点$(-1,2)$,则$k$的值为(
A.6
B.-6
C.2
D.-2
D
)A.6
B.-6
C.2
D.-2
答案:D
解析:
将正比例函数$y = kx$的图象向右平移2个单位长度,根据“左加右减”原则,得到$y = k(x - 2)$;再向下平移4个单位长度,根据“上加下减”原则,得到平移后的函数解析式为$y = k(x - 2)-4$。
因为平移后的图象经过点$(-1,2)$,将$x=-1$,$y=2$代入$y = k(x - 2)-4$,可得:
$2 = k(-1 - 2)-4$
$2 = -3k - 4$
$-3k = 2 + 4$
$-3k = 6$
$k = -2$
D
因为平移后的图象经过点$(-1,2)$,将$x=-1$,$y=2$代入$y = k(x - 2)-4$,可得:
$2 = k(-1 - 2)-4$
$2 = -3k - 4$
$-3k = 2 + 4$
$-3k = 6$
$k = -2$
D
8. 在平面直角坐标系中,把正比例函数$y= -3x的图象向上平移后得到直线AB$,若直线$AB经过点(m,n)$,且$3m+n= 4$,则直线$AB$对应的函数表达式是(
A.$y= -3x+4$
B.$y= -3x-4$
C.$y= 3x+4$
D.$y= 3x-4$
A
)A.$y= -3x+4$
B.$y= -3x-4$
C.$y= 3x+4$
D.$y= 3x-4$
答案:A
解析:
设直线$AB$对应的函数表达式为$y = -3x + b$。
因为直线$AB$经过点$(m,n)$,所以$n=-3m + b$,即$3m + n = b$。
已知$3m + n = 4$,所以$b = 4$。
故直线$AB$对应的函数表达式是$y=-3x + 4$。
A
因为直线$AB$经过点$(m,n)$,所以$n=-3m + b$,即$3m + n = b$。
已知$3m + n = 4$,所以$b = 4$。
故直线$AB$对应的函数表达式是$y=-3x + 4$。
A