8. 甲、乙两物体分别在水平拉力作用下做匀速直线运动。如果甲所受的水平拉力是乙的2倍,甲移动的距离是乙的3倍,那么水平拉力对甲、乙两物体所做的功之比为(
A.24∶1
B.12∶1
C.6∶1
D.2∶1
C
)。A.24∶1
B.12∶1
C.6∶1
D.2∶1
答案:C
解析:
设乙所受水平拉力为$F$,则甲所受水平拉力为$2F$;设乙移动的距离为$s$,则甲移动的距离为$3s$。
拉力对甲做的功$W_{甲}=2F×3s = 6Fs$,
拉力对乙做的功$W_{乙}=F× s=Fs$,
所以$W_{甲}:W_{乙}=6Fs:Fs = 6:1$。
C
拉力对甲做的功$W_{甲}=2F×3s = 6Fs$,
拉力对乙做的功$W_{乙}=F× s=Fs$,
所以$W_{甲}:W_{乙}=6Fs:Fs = 6:1$。
C
9. 如图11-5-3所示,一个人先后用同样大小的力F将不同质量的物体分别在光滑水平面、粗糙水平面和粗糙斜面上沿力的方向移动相同的距离s,该力在这三个过程中所做的功分别为$W_1、$$W_2、$$W_3。$关于它们之间的大小关系,下列说法中正确的是(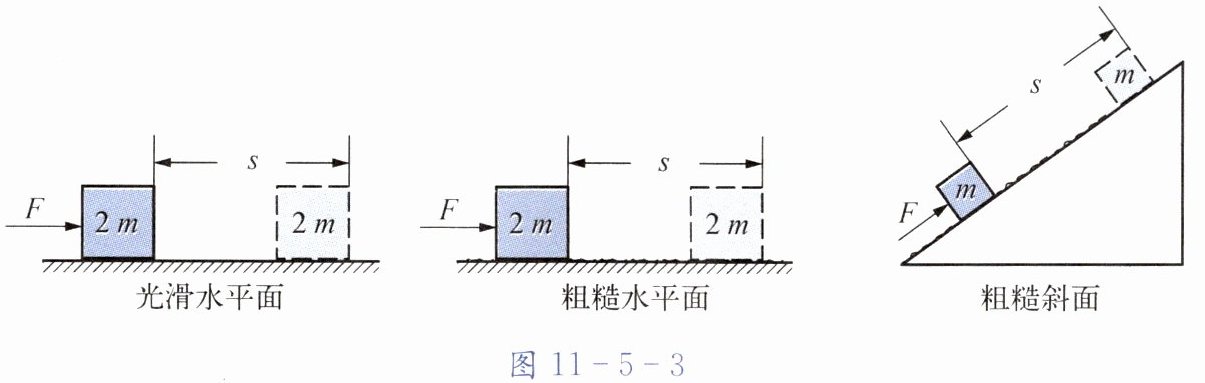
$A. W_1<W_2<W_3$
$B. W_1<W_2=W_3$
$C. W_1=W_2=W_3$
$D. W_1=W_2<W_3$
C
)。
$A. W_1<W_2<W_3$
$B. W_1<W_2=W_3$
$C. W_1=W_2=W_3$
$D. W_1=W_2<W_3$
答案:C
解析:
根据功的计算公式$W = Fs$,在三个过程中,力$F$的大小相同,物体沿力的方向移动的距离$s$也相同,所以$W_1 = Fs$,$W_2 = Fs$,$W_3 = Fs$,故$W_1 = W_2 = W_3$。
C
C
10. 如图11-5-4所示,某工人将重为150 N的木块竖直向上匀速提升4 m,若滑轮重为10 N,则该工人的拉力所做的功为
640
J。(绳重、滑轮轴间摩擦忽略不计)答案:640
解析:
由图可知,该滑轮为动滑轮,承担物重的绳子段数$n=2$。
绳重、滑轮轴间摩擦忽略不计,工人的拉力$F = \frac{G_{物} + G_{轮}}{n} = \frac{150\ N + 10\ N}{2} = 80\ N$。
拉力端移动的距离$s = nh = 2 × 4\ m = 8\ m$。
拉力所做的功$W = Fs = 80\ N × 8\ m = 640\ J$。
640
绳重、滑轮轴间摩擦忽略不计,工人的拉力$F = \frac{G_{物} + G_{轮}}{n} = \frac{150\ N + 10\ N}{2} = 80\ N$。
拉力端移动的距离$s = nh = 2 × 4\ m = 8\ m$。
拉力所做的功$W = Fs = 80\ N × 8\ m = 640\ J$。
640
11. 小明用500 N的力匀速举高杠铃,若他所做的功为250 J,则小明举高杠铃的高度是多少?
答案:F=G=500 N,s=$\frac{W}{F}$=0.5 m
解析:
已知$F = 500\ N$,$W = 250\ J$,根据$W = Fs$,可得$s=\frac{W}{F}=\frac{250\ J}{500\ N} = 0.5\ m$。
12. 某同学用已校正好的弹簧测力计测量一个放在水平桌面上的钩码的重力。他从图11-5-5(a)所示位置(此时指针指0刻度线)开始将弹簧测力计缓慢竖直向上提起,记下弹簧测力计移动的距离h和对应的读数F,并描出F-h图像如图11-5-5(b)所示。
(1)钩码的重力为______N。
(2)请分析h在下列两个区间内弹簧测力计的拉力对钩码做功的情况,若做功,请计算做功的数值。
① 0~5 cm区间:______。
② 5~15 cm区间:______。
[答案]:(1)

(1)钩码的重力为______N。
(2)请分析h在下列两个区间内弹簧测力计的拉力对钩码做功的情况,若做功,请计算做功的数值。
① 0~5 cm区间:______。
② 5~15 cm区间:______。
[答案]:(1)
4
(2)① 弹簧测力计对钩码不做功
② 弹簧测力计对钩码所做的功为0.4 J
答案:(1)4 (2)① 弹簧测力计对钩码不做功 ② 弹簧测力计对钩码所做的功为0.4 J
解析:
(1)4
(2)①弹簧测力计对钩码不做功
②$W=Fs=4\ N×(0.15\ m-0.05\ m)=0.4\ J$