23.(6分)如图所示,小明在做“比较不同液体吸热能力”的实验时,使用相同的电加热器给两种不同种类的液体a和b加热。
|实验序号|液体|质量m/kg|升高的温度Δt/℃|加热的时间t/min|
|①|a|0.1|5|1|
|②|a|0.1|10|2|
|③|a|0.2|10|4|
|④|b|0.1|10|1|
|⑤|b|0.1|20|2|
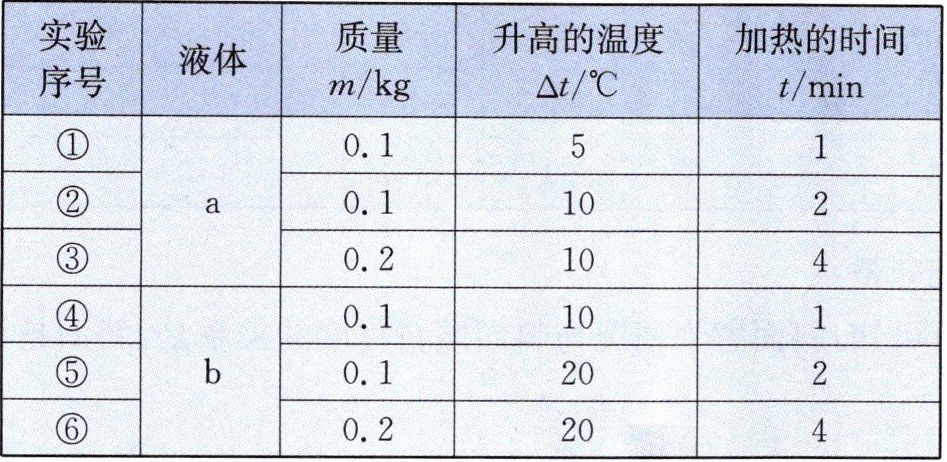
|⑥|b|0.2|20|4|
(1)分析第①、④次,第②、⑤次或第③、⑥次实验数据,小明认为：加热时间相同时,液体b升高的温度高一些,这说明液体b吸收的热量多一些。小明的判断是否正确？请说明理由：______。
(2)分析第②、③次或第⑤、⑥次实验数据,可以得出的初步结论是：同种物质升高相同温度时,物质的______越大,吸收的热量越______(多/少)。
(3)通过比较第②、④次实验数据可知,液体吸收的热量多少与液体的______有关,液体______(a/b)的吸热能力更强。
|实验序号|液体|质量m/kg|升高的温度Δt/℃|加热的时间t/min|
|①|a|0.1|5|1|
|②|a|0.1|10|2|
|③|a|0.2|10|4|
|④|b|0.1|10|1|
|⑤|b|0.1|20|2|
|⑥|b|0.2|20|4|
(1)分析第①、④次,第②、⑤次或第③、⑥次实验数据,小明认为：加热时间相同时,液体b升高的温度高一些,这说明液体b吸收的热量多一些。小明的判断是否正确？请说明理由：______。
(2)分析第②、③次或第⑤、⑥次实验数据,可以得出的初步结论是：同种物质升高相同温度时,物质的______越大,吸收的热量越______(多/少)。
(3)通过比较第②、④次实验数据可知,液体吸收的热量多少与液体的______有关,液体______(a/b)的吸热能力更强。
答案：
（1）不正确 实验中使用的电加热器相同，加热相同的时间，a、b两种液体吸收的热量相等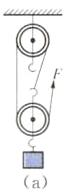
（2）质量 多 （3）种类 a
（1）不正确 实验中使用的电加热器相同，加热相同的时间，a、b两种液体吸收的热量相等
（2）质量 多 （3）种类 a24.(4分)某建筑工地用如图所示的简易滑轮组将重为4000 N的砖块运到离地4 m高处,已知每个滑轮重100 N,滑轮摩擦和绳重以及动滑轮下的篮子的重力忽略不计。若提升砖块的工人作用于绳的拉力最大为500 N,求：
(1)每次提升砖块的最大重力和最大机械效率。
(2)若全部完成提升砖块任务,则工人利用此滑轮组至少做多少额外功？
(1)每次提升砖块的最大重力和最大机械效率。
(2)若全部完成提升砖块任务,则工人利用此滑轮组至少做多少额外功？
答案：（1）900 N 90% （2）2000 J
解析：
（1）由图知，承担物重的绳子段数$n=2$。
因为滑轮摩擦和绳重以及篮子重力忽略不计，所以$F = \frac{G + G_{动}}{n}$，则每次提升砖块的最大重力$G = nF - G_{动} = 2×500N - 100N = 900N$。
最大机械效率$\eta=\frac{W_{有}}{W_{总}}×100\%=\frac{Gh}{Fs}×100\%=\frac{Gh}{Fnh}×100\%=\frac{G}{nF}×100\%=\frac{900N}{2×500N}×100\% = 90\%$。
（2）总共需要提升的砖块重力为$4000N$，每次最大提升$900N$，则需要提升的次数$n=\lceil\frac{4000N}{900N}\rceil = 5$（次）（向上取整）。
每次提升动滑轮做的额外功$W_{额1}=G_{动}h = 100N×4m = 400J$，所以至少做的额外功$W_{额}=nW_{额1}=5×400J = 2000J$。
（1）$900N$；$90\%$
（2）$2000J$
因为滑轮摩擦和绳重以及篮子重力忽略不计，所以$F = \frac{G + G_{动}}{n}$，则每次提升砖块的最大重力$G = nF - G_{动} = 2×500N - 100N = 900N$。
最大机械效率$\eta=\frac{W_{有}}{W_{总}}×100\%=\frac{Gh}{Fs}×100\%=\frac{Gh}{Fnh}×100\%=\frac{G}{nF}×100\%=\frac{900N}{2×500N}×100\% = 90\%$。
（2）总共需要提升的砖块重力为$4000N$，每次最大提升$900N$，则需要提升的次数$n=\lceil\frac{4000N}{900N}\rceil = 5$（次）（向上取整）。
每次提升动滑轮做的额外功$W_{额1}=G_{动}h = 100N×4m = 400J$，所以至少做的额外功$W_{额}=nW_{额1}=5×400J = 2000J$。
（1）$900N$；$90\%$
（2）$2000J$
25.(10分)太阳能热水器是生活中常见的一种利用太阳能的装置。某款太阳能热水器平均每小时接收$4.2×10^6 J$的太阳能,在5 h的有效照射时间内,能够将热水器中质量为100 kg、初温为20 ℃的水温度升高到40 ℃。
(1)此热水器5 h内接收到多少焦的太阳能？
(2)此热水器中的水增加的内能是多少？[水的比热容$c= 4.2×10^3 J/(kg·℃)] $
(3)此热水器的效率为多大？
(4)若用另一台燃气热水器提供相同的热水,不考虑热量的损失,则需要完全燃烧多少千克天然气？(天然气的热值$q= 4.2×10^7 J/kg,$假设天然气燃烧放出的热量全部被水吸收)
(5)太阳能热水器与燃气热水器相比有哪些优点？(请至少写出两点)
(1)此热水器5 h内接收到多少焦的太阳能？
(2)此热水器中的水增加的内能是多少？[水的比热容$c= 4.2×10^3 J/(kg·℃)] $
(3)此热水器的效率为多大？
(4)若用另一台燃气热水器提供相同的热水,不考虑热量的损失,则需要完全燃烧多少千克天然气？(天然气的热值$q= 4.2×10^7 J/kg,$假设天然气燃烧放出的热量全部被水吸收)
(5)太阳能热水器与燃气热水器相比有哪些优点？(请至少写出两点)
答案：（1）$2.1× 10^{7}\ J$ （2）$8.4× 10^{6}\ J$ （3）40% （4）0.2 kg （5）无污染，安全可靠，节约能源，经济实惠
解析：
(1) 热水器5小时内接收到的太阳能：$Q_{太} = 4.2 × 10^6\ J/h × 5\ h = 2.1 × 10^7\ J$
(2) 水吸收的热量（即增加的内能）：$Q_{吸} = cm\Delta t = 4.2 × 10^3\ J/(kg·℃) × 100\ kg × (40\ ℃ - 20\ ℃) = 8.4 × 10^6\ J$
(3) 热水器的效率：$\eta = \frac{Q_{吸}}{Q_{太}} × 100\% = \frac{8.4 × 10^6\ J}{2.1 × 10^7\ J} × 100\% = 40\%$
(4) 天然气完全燃烧放出的热量：$Q_{放} = Q_{吸} = 8.4 × 10^6\ J$，需要天然气的质量：$m = \frac{Q_{放}}{q} = \frac{8.4 × 10^6\ J}{4.2 × 10^7\ J/kg} = 0.2\ kg$
(5) 无污染，节约能源