4. 如图,AB= AD,∠C= ∠E,且∠BAE= ∠DAC.求证:△ABC≌△ADE.

答案:【解析】:本题考查全等三角形的判定定理。题目已知条件有$AB = AD$,$\angle C=\angle E$,$\angle BAE=\angle DAC$,需要通过这些条件证明$\triangle ABC\cong\triangle ADE$。我们可以通过对$\angle BAE=\angle DAC$进行等式变形,得到一组相等的角,再结合已知的边和角,利用“$AAS$”(两角及其中一角的对边对应相等的两个三角形全等)来证明两个三角形全等。
【答案】:证明:
∵$\angle BAE=\angle DAC$,
∴$\angle BAE-\angle CAE=\angle DAC - \angle CAE$(等式两边同时减去同一个角$\angle CAE$),
即$\angle BAC=\angle DAE$。
在$\triangle ABC$和$\triangle ADE$中,
$\begin{cases}\angle C=\angle E\\\angle BAC=\angle DAE\\AB = AD\end{cases}$
∴$\triangle ABC\cong\triangle ADE(AAS)$。
【答案】:证明:
∵$\angle BAE=\angle DAC$,
∴$\angle BAE-\angle CAE=\angle DAC - \angle CAE$(等式两边同时减去同一个角$\angle CAE$),
即$\angle BAC=\angle DAE$。
在$\triangle ABC$和$\triangle ADE$中,
$\begin{cases}\angle C=\angle E\\\angle BAC=\angle DAE\\AB = AD\end{cases}$
∴$\triangle ABC\cong\triangle ADE(AAS)$。
5. 如图,AD//BC,∠BAD= 90°,以点B为圆心,BC长为半径画弧,与AD相交于点E,连接BE,过点C作CF⊥BE,垂足为F.线段BF与图中已有的哪一条线段相等?将猜想出的结论填写在下面的横线上并证明.
结论:BF=

结论:BF=
AB
.
答案:BF=AB
证明:∵AD//BC,
∴∠AEB=∠FBC。
∵∠BAD=90°,CF⊥BE,
∴∠BAE=∠CFB=90°。
∵以点B为圆心,BC长为半径画弧,与AD相交于点E,
∴BE=BC。
在△BAE和△CFB中,
∠AEB=∠FBC,
∠BAE=∠CFB,
BE=CB,
∴△BAE≌△CFB(AAS),
∴BF=AB。
证明:∵AD//BC,
∴∠AEB=∠FBC。
∵∠BAD=90°,CF⊥BE,
∴∠BAE=∠CFB=90°。
∵以点B为圆心,BC长为半径画弧,与AD相交于点E,
∴BE=BC。
在△BAE和△CFB中,
∠AEB=∠FBC,
∠BAE=∠CFB,
BE=CB,
∴△BAE≌△CFB(AAS),
∴BF=AB。
6. 如图,在△ABC中,AD是∠BAC的平分线,点E,F分别在边AB,AC上,∠AED= ∠CFD.求证:DE= DF.


答案:证明:
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD。
在△AED和△AFD中,
∠AED=∠CFD(已知),
∠BAD=∠CAD(已证),
AD=AD(公共边),
∴△AED≌△AFD(AAS)。
∴DE=DF。
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD。
在△AED和△AFD中,
∠AED=∠CFD(已知),
∠BAD=∠CAD(已证),
AD=AD(公共边),
∴△AED≌△AFD(AAS)。
∴DE=DF。
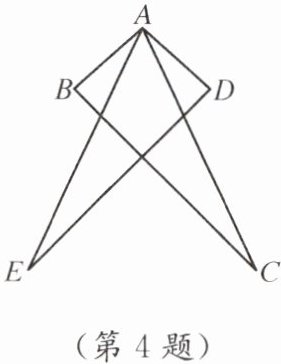
7. 如图,∠D= ∠BAC= ∠E,AB= AC.探索DE,BD,CE之间的长度关系,并说明理由.


答案:【解析】:本题可根据已知条件,通过证明三角形全等,进而得出线段之间的长度关系。考查的知识点是全等三角形的判定与性质。解题的关键在于利用给定的角相等关系以及边的条件,构造出全等三角形。
【答案】:解:$DE = BD + CE$。理由如下:
∵$\angle D=\angle BAC=\angle E$,$\angle BAD+\angle CAE = 180^{\circ}-\angle BAC$,$\angle CAE+\angle ECA = 180^{\circ}-\angle E$,且$\angle BAC=\angle E$,
∴$\angle BAD=\angle ECA$。
在$\triangle ABD$和$\triangle CAE$中,
$\begin{cases}\angle D=\angle E\\\angle BAD=\angle ECA\\AB = AC\end{cases}$
∴$\triangle ABD\cong\triangle CAE(AAS)$。
∴$BD = AE$,$AD = CE$。
∵$DE=AD + AE$,
∴$DE = BD + CE$。
【答案】:解:$DE = BD + CE$。理由如下:
∵$\angle D=\angle BAC=\angle E$,$\angle BAD+\angle CAE = 180^{\circ}-\angle BAC$,$\angle CAE+\angle ECA = 180^{\circ}-\angle E$,且$\angle BAC=\angle E$,
∴$\angle BAD=\angle ECA$。
在$\triangle ABD$和$\triangle CAE$中,
$\begin{cases}\angle D=\angle E\\\angle BAD=\angle ECA\\AB = AC\end{cases}$
∴$\triangle ABD\cong\triangle CAE(AAS)$。
∴$BD = AE$,$AD = CE$。
∵$DE=AD + AE$,
∴$DE = BD + CE$。