3. 如图,平移、轴对称、旋转前后的图形全等,根据全等三角形写出对应的边和角.
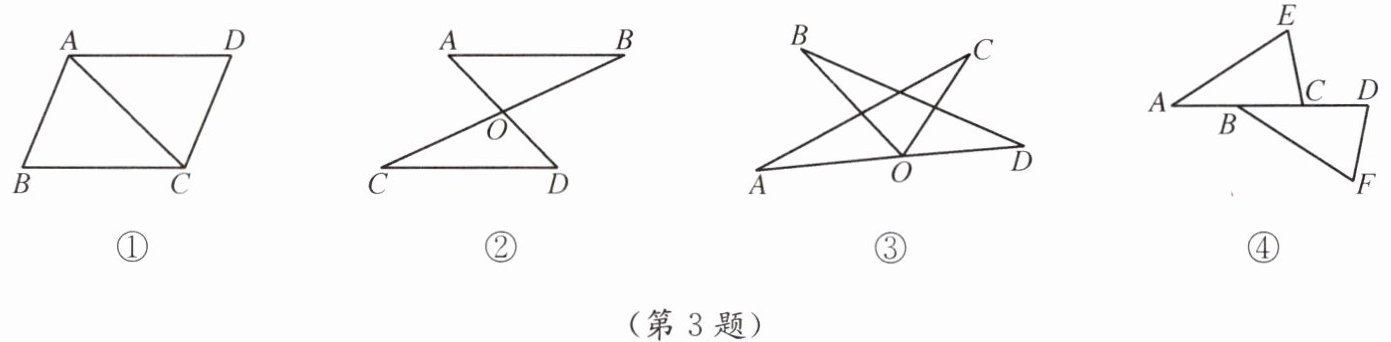
(1)如图①,△ABC≌△CDA,AB的对应边是
(2)如图②,△AOB≌△DOC,OA的对应边是
(3)如图③,△AOC≌△BOD,AC的对应边是
(4)如图④,△ACE≌△BDF,AC的对应边是

(1)如图①,△ABC≌△CDA,AB的对应边是
CD
,∠BAC的对应角是∠DCA
;(2)如图②,△AOB≌△DOC,OA的对应边是
OD
,∠B的对应角是∠C
;(3)如图③,△AOC≌△BOD,AC的对应边是
BD
,∠C的对应角是∠D
;(4)如图④,△ACE≌△BDF,AC的对应边是
BD
,∠ACE的对应角是∠BDF
.答案:【解析】:
本题考查了全等三角形的对应边和对应角的识别,需要利用全等三角形的性质,即全等三角形的对应边相等,对应角相等,通过观察图形,确定每个全等三角形中的对应边和对应角。
【答案】:
(1) $CD$;$\angle DCA$
(2) $OD$;$\angle C$
(3) $BD$;$\angle D$
(4) $BD$;$\angle BDF$
本题考查了全等三角形的对应边和对应角的识别,需要利用全等三角形的性质,即全等三角形的对应边相等,对应角相等,通过观察图形,确定每个全等三角形中的对应边和对应角。
【答案】:
(1) $CD$;$\angle DCA$
(2) $OD$;$\angle C$
(3) $BD$;$\angle D$
(4) $BD$;$\angle BDF$
4. 如图,△ABD≌△ACE.求证:BE= CD.


答案:【解析】:
本题考查全等三角形的性质,利用全等三角形的对应边相等这一性质,通过线段的转化来证明$BE = CD$。
已知$\triangle ABD\cong\triangle ACE$,根据全等三角形的性质,全等三角形的对应边相等,对应角相等。
在$\triangle ABD$和$\triangle ACE$中,$AB$与$AC$,$AE$与$AD$分别是对应边,所以可得$AB = AC$,$AE = AD$。
因为$BE=AB - AE$,$CD = AC - AD$,又因为$AB = AC$,$AE = AD$,所以$AB - AE=AC - AD$,即$BE = CD$。
【答案】:
证明:
∵$\triangle ABD\cong\triangle ACE$,
∴$AB = AC$,$AE = AD$,
∴$AB - AE=AC - AD$,
即$BE = CD$。
本题考查全等三角形的性质,利用全等三角形的对应边相等这一性质,通过线段的转化来证明$BE = CD$。
已知$\triangle ABD\cong\triangle ACE$,根据全等三角形的性质,全等三角形的对应边相等,对应角相等。
在$\triangle ABD$和$\triangle ACE$中,$AB$与$AC$,$AE$与$AD$分别是对应边,所以可得$AB = AC$,$AE = AD$。
因为$BE=AB - AE$,$CD = AC - AD$,又因为$AB = AC$,$AE = AD$,所以$AB - AE=AC - AD$,即$BE = CD$。
【答案】:
证明:
∵$\triangle ABD\cong\triangle ACE$,
∴$AB = AC$,$AE = AD$,
∴$AB - AE=AC - AD$,
即$BE = CD$。
5. 如图,△ACE≌△DBF,AD= 8,BC= 2.
(1)求AC的长度;
(2)求证:CE//BF.

(1)求AC的长度;
(2)求证:CE//BF.

答案:(1)解:∵△ACE≌△DBF,
∴AC=DB,
∵AC=AB+BC,DB=DC+BC,
∴AB=DC,
∵AD=AB+BC+CD=8,BC=2,
∴AB+CD=8-2=6,
∴AB=CD=3,
∴AC=AB+BC=3+2=5;
(2)证明:∵△ACE≌△DBF,
∴∠ACE=∠DBF,
∴CE//BF.
∴AC=DB,
∵AC=AB+BC,DB=DC+BC,
∴AB=DC,
∵AD=AB+BC+CD=8,BC=2,
∴AB+CD=8-2=6,
∴AB=CD=3,
∴AC=AB+BC=3+2=5;
(2)证明:∵△ACE≌△DBF,
∴∠ACE=∠DBF,
∴CE//BF.
6. 如图,点A,B,C在一条直线上,点E在边BD上,且△ABD≌△EBC,AB= 2 cm,BC= 3 cm.
(1)求DE的长;
(2)判断AC与BD的位置关系,并说明理由;
(3)判断直线AD与直线CE的位置关系,并说明理由.

(1)求DE的长;
(2)判断AC与BD的位置关系,并说明理由;
(3)判断直线AD与直线CE的位置关系,并说明理由.

答案:(1)解:∵△ABD≌△EBC,
∴AB=EB=2cm,BD=BC=3cm,
∵DE=BD-EB,
∴DE=3-2=1cm。
(2)解:AC⊥BD。理由如下:
∵△ABD≌△EBC,
∴∠ABD=∠EBC,
∵点A,B,C在一条直线上,
∴∠ABD+∠EBC=180°,
∴∠ABD=∠EBC=90°,
∴AC⊥BD。
(3)解:AD⊥CE。理由如下:
延长CE交AD于点F,
∵△ABD≌△EBC,
∴∠D=∠C,
∵∠ABD=90°,
∴∠A+∠D=90°,
∴∠A+∠C=90°,
∴∠AFC=90°,
∴AD⊥CE。
∴AB=EB=2cm,BD=BC=3cm,
∵DE=BD-EB,
∴DE=3-2=1cm。
(2)解:AC⊥BD。理由如下:
∵△ABD≌△EBC,
∴∠ABD=∠EBC,
∵点A,B,C在一条直线上,
∴∠ABD+∠EBC=180°,
∴∠ABD=∠EBC=90°,
∴AC⊥BD。
(3)解:AD⊥CE。理由如下:
延长CE交AD于点F,
∵△ABD≌△EBC,
∴∠D=∠C,
∵∠ABD=90°,
∴∠A+∠D=90°,
∴∠A+∠C=90°,
∴∠AFC=90°,
∴AD⊥CE。