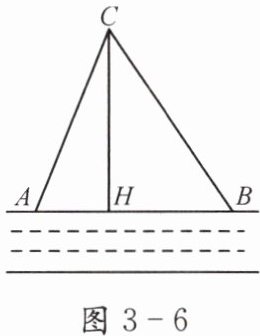
如图3-6,在一条东西走向的河流的一侧有一村庄C,河边原有两个取水点A,B,且AB= AC.由于某种原因,C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A,H,B在同一条直线上),并新修一条路CH,测得CB= 1.5 km,CH= 1.2 km,HB= 0.9 km. CH是否为从村庄C到河边的最近路?如果是,新路CH比原路CA短多少千米?

答案:解:在△CHB中,CH=1.2km,HB=0.9km,CB=1.5km
∵CH²+HB²=1.2²+0.9²=1.44+0.81=2.25,CB²=1.5²=2.25
∴CH²+HB²=CB²
∴△CHB是直角三角形,∠CHB=90°
∴CH⊥AB
∵点到直线的距离中,垂线段最短
∴CH是从村庄C到河边的最近路
设AC=AB=x km,则AH=AB-HB=(x-0.9)km
在Rt△AHC中,AH²+CH²=AC²
即(x-0.9)²+1.2²=x²
展开得x²-1.8x+0.81+1.44=x²
化简得-1.8x+2.25=0
解得x=1.25
∴AC=1.25km
∴AC-CH=1.25-1.2=0.05km
答:CH是从村庄C到河边的最近路,新路CH比原路CA短0.05千米。
∵CH²+HB²=1.2²+0.9²=1.44+0.81=2.25,CB²=1.5²=2.25
∴CH²+HB²=CB²
∴△CHB是直角三角形,∠CHB=90°
∴CH⊥AB
∵点到直线的距离中,垂线段最短
∴CH是从村庄C到河边的最近路
设AC=AB=x km,则AH=AB-HB=(x-0.9)km
在Rt△AHC中,AH²+CH²=AC²
即(x-0.9)²+1.2²=x²
展开得x²-1.8x+0.81+1.44=x²
化简得-1.8x+2.25=0
解得x=1.25
∴AC=1.25km
∴AC-CH=1.25-1.2=0.05km
答:CH是从村庄C到河边的最近路,新路CH比原路CA短0.05千米。
例1 我国古代数学著作《九章算术》中记载了一道有趣的问题.如图3-7,有一个水池,水面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇垂直拉向岸边,那么它的顶端恰好到达岸边的水面.这个水池的深度和这根芦苇的长度各是多少?


答案:解:设水池的深度为$x$尺,则芦苇的长度为$(x + 1)$尺。
由题意知,水面是边长为10尺的正方形,芦苇在水池正中央,所以芦苇到岸边的水平距离为$\frac{10}{2}=5$尺。
根据勾股定理,得$x^{2}+5^{2}=(x + 1)^{2}$。
展开得$x^{2}+25=x^{2}+2x + 1$。
移项、合并同类项得$2x=24$。
解得$x = 12$。
芦苇长度为$x+1=12 + 1=13$(尺)。
答:水池的深度为12尺,芦苇的长度为13尺。
由题意知,水面是边长为10尺的正方形,芦苇在水池正中央,所以芦苇到岸边的水平距离为$\frac{10}{2}=5$尺。
根据勾股定理,得$x^{2}+5^{2}=(x + 1)^{2}$。
展开得$x^{2}+25=x^{2}+2x + 1$。
移项、合并同类项得$2x=24$。
解得$x = 12$。
芦苇长度为$x+1=12 + 1=13$(尺)。
答:水池的深度为12尺,芦苇的长度为13尺。
例2 某校修建如图3-8①所示的自行车棚,钢架已完成.现需要在棚顶覆盖铁皮,图3-8②是自行车棚顶的示意图.
已知AD= BD,CD⊥AB,垂足为C,棚宽AB= 6 m,棚高CD= 1.6 m,棚长BE= 20 m,学校打算在校园的不同角落修建一模一样的五个车棚.求覆盖一个车棚顶需要的铁皮面积(车棚顶铁皮褶皱忽略不计,车棚顶最顶端梁脊不用铁皮).

已知AD= BD,CD⊥AB,垂足为C,棚宽AB= 6 m,棚高CD= 1.6 m,棚长BE= 20 m,学校打算在校园的不同角落修建一模一样的五个车棚.求覆盖一个车棚顶需要的铁皮面积(车棚顶铁皮褶皱忽略不计,车棚顶最顶端梁脊不用铁皮).

答案:解:∵AD=BD,CD⊥AB,AB=6m,
∴AC=BC=3m。
在Rt△ACD中,AC=3m,CD=1.6m,
由勾股定理得:AD=$\sqrt{AC^2 + CD^2}=\sqrt{3^2 + 1.6^2}=\sqrt{9 + 2.56}=\sqrt{11.56}=3.4$m。
车棚顶为平行四边形ABED,其面积=AD×BE=3.4×20=68m²。
答:覆盖一个车棚顶需要的铁皮面积为68m²。
∴AC=BC=3m。
在Rt△ACD中,AC=3m,CD=1.6m,
由勾股定理得:AD=$\sqrt{AC^2 + CD^2}=\sqrt{3^2 + 1.6^2}=\sqrt{9 + 2.56}=\sqrt{11.56}=3.4$m。
车棚顶为平行四边形ABED,其面积=AD×BE=3.4×20=68m²。
答:覆盖一个车棚顶需要的铁皮面积为68m²。