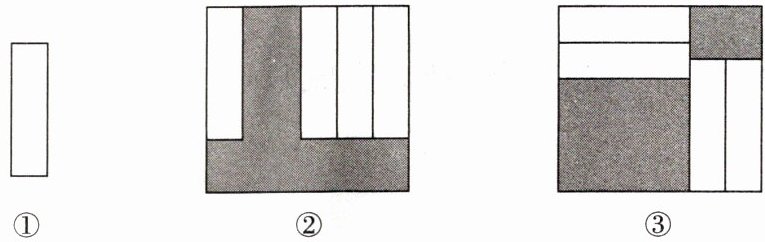
如图,把四张大小相同的长方形卡片(如图①)按图②、图③两种方式放在一个底面为长方形(长比宽多$5cm$)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为$C_{1}$,图③中阴影部分的周长为$C_{2}$,那么$C_{1}比C_{2}$大
]
10
$cm$。]

答案:10
解析:
设长方形卡片的长为$a\ cm$,宽为$b\ cm$,盒底的宽为$m\ cm$,则盒底的长为$(m + 5)\ cm$。
由图②,得$a + 2b = m + 5$,$2b = m$,则$a = 5$。
$C_{1}=2[(m + 5)+m]=4m + 10$。
由图③,阴影部分周长等于盒底周长,$C_{2}=2[(m + 5)+m]=4m + 10$。
$C_{1}-C_{2}=(4m + 10)-(4m + 10)=0$。
1
由图②,得$a + 2b = m + 5$,$2b = m$,则$a = 5$。
$C_{1}=2[(m + 5)+m]=4m + 10$。
由图③,阴影部分周长等于盒底周长,$C_{2}=2[(m + 5)+m]=4m + 10$。
$C_{1}-C_{2}=(4m + 10)-(4m + 10)=0$。
1
1. 已知$(4x^{2} - 7x - 3) - A = 3x^{2} - 2x + 1$,则$A$为(
A.$x^{2} - 9x + 2$
B.$x^{2} - 9x - 4$
C.$x^{2} - 5x - 2$
D.$x^{2} - 5x - 4$
D
)A.$x^{2} - 9x + 2$
B.$x^{2} - 9x - 4$
C.$x^{2} - 5x - 2$
D.$x^{2} - 5x - 4$
答案:D
解析:
由题意得,$A=(4x^{2}-7x-3)-(3x^{2}-2x+1)$
$=4x^{2}-7x-3-3x^{2}+2x-1$
$=(4x^{2}-3x^{2})+(-7x+2x)+(-3-1)$
$=x^{2}-5x-4$
D
$=4x^{2}-7x-3-3x^{2}+2x-1$
$=(4x^{2}-3x^{2})+(-7x+2x)+(-3-1)$
$=x^{2}-5x-4$
D
2. 已知一个长方形的周长为$(4a + 2b)$,宽为$(a - b)$,则它的长为(
A.$a + 2b$
B.$a$
C.$3a + 3b$
D.$3a + b$
A
)A.$a + 2b$
B.$a$
C.$3a + 3b$
D.$3a + b$
答案:A
解析:
长方形周长公式:周长 = 2×(长 + 宽)。
已知周长为 $4a + 2b$,宽为 $a - b$,设长为 $x$,则:
$4a + 2b = 2(x + a - b)$
等式两边同除以2:$2a + b = x + a - b$
移项得:$x = 2a + b - a + b = a + 2b$
答案:A
已知周长为 $4a + 2b$,宽为 $a - b$,设长为 $x$,则:
$4a + 2b = 2(x + a - b)$
等式两边同除以2:$2a + b = x + a - b$
移项得:$x = 2a + b - a + b = a + 2b$
答案:A
3. 填空:
(1) 单项式$-3x^{2}$,$5x$,$2x^{2}$,$-2x$的和是
(2) 比$3 - x^{2} + x少x^{3} + 5x$的多项式是
(3) 老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了如右图所示的一个二次三项式,则所捂的二次三项式是
(4) 已知$2x - 3y = 1$,则$10 - 4x + 6y = $

(1) 单项式$-3x^{2}$,$5x$,$2x^{2}$,$-2x$的和是
$3x-x^2$
;(2) 比$3 - x^{2} + x少x^{3} + 5x$的多项式是
$-x^3-x^2-4x+3$
;(3) 老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了如右图所示的一个二次三项式,则所捂的二次三项式是
$x^2-2x+1$
;(4) 已知$2x - 3y = 1$,则$10 - 4x + 6y = $
8
。
答案:(1)$3x-x^2$;(2)$-x^3-x^2-4x+3$;(3)$x^2-2x+1$;(4)8.
解析:
(1)$3x - x^{2}$
(2)$-x^{3} - x^{2} - 4x + 3$
(3)$x^{2} - 2x + 1$
(4)$8$
4. 计算:
(1) 先化简$2(3a^{2}b - ab^{2}) - 3(-ab^{2} + 2a^{2}b)$,并求当$a = 2$,$b = -3$时的值。
(2) 已知$A = 2x^{2} - 3x - 5$,$B = -x^{2} + 2x - 3$,求$A - 2B$。
(1) 先化简$2(3a^{2}b - ab^{2}) - 3(-ab^{2} + 2a^{2}b)$,并求当$a = 2$,$b = -3$时的值。
(2) 已知$A = 2x^{2} - 3x - 5$,$B = -x^{2} + 2x - 3$,求$A - 2B$。
答案:(1)原式$=6a^2b-2ab^2+3ab^2-6a^2b=ab^2$,当$a=2,b=-3$时,原式$=2×(-3)^2=18$. (2)$A-2B=2x^2-3x-5-2(-x^2+2x-3)=2x^2-3x-5+2x^2-4x+6=4x^2-7x+1$.