2. 如图6-5,$∠AOD= ∠AOB+∠$
BOD
$=∠AOE-∠$DOE
$=∠COD+∠$AOC
$=∠BOE+∠$AOB
$-∠$DOE
.答案:BOD
DOE
AOC
AOB
DOE
DOE
AOC
AOB
DOE
1. 有下列说法:①两条射线所组成的图形叫作角;②一条射线旋转而成的图形叫作角;③两边成一条直线的角是平角;④平角是一条直线. 其中,正确的有 (
A.1个
B.2个
C.3个
D.4个
A
)A.1个
B.2个
C.3个
D.4个
答案:A
解析:
①两条射线需有公共端点所组成的图形叫作角,故①错误;
②一条射线绕着它的端点旋转而成的图形叫作角,故②错误;
③两边成一条直线的角是平角,故③正确;
④平角是由一条射线绕端点旋转180度形成的角,不是一条直线,故④错误。
正确的有1个。
A
②一条射线绕着它的端点旋转而成的图形叫作角,故②错误;
③两边成一条直线的角是平角,故③正确;
④平角是由一条射线绕端点旋转180度形成的角,不是一条直线,故④错误。
正确的有1个。
A
2. 如图,写出符合下列条件的角:
(1)能用一个大写字母表示的角有
(2)以B为顶点的角有
(3)以CD为边的角有
(1)能用一个大写字母表示的角有
∠A,∠C
;(2)以B为顶点的角有
∠1,∠2,∠ABC
(用较简洁的方法表示);(3)以CD为边的角有
∠C,∠α,∠ADC
.答案:∠A,∠C
∠1,∠2,∠ABC
∠C,∠α,∠ADC
∠1,∠2,∠ABC
∠C,∠α,∠ADC
解析:
(1)在顶点处只有一个角存在时,才能用一个字母来表示这个角,否则分不清表示哪一个角,当顶点处不止一个角时,不能用一个大写字母表示,观察图形可知能用一个大写字母表示的角有$\angle A$,$\angle C$;
(2)以B为顶点的角有3个,可用三个大写字母表示为$\angle 1$,$\angle 2$,$\angle ABC$;
(3)以CD为边的角有4个,分别为$\angle 2$,$\angle 3$,$\angle BCD$,$\angle \alpha $。
(2)以B为顶点的角有3个,可用三个大写字母表示为$\angle 1$,$\angle 2$,$\angle ABC$;
(3)以CD为边的角有4个,分别为$\angle 2$,$\angle 3$,$\angle BCD$,$\angle \alpha $。
3. $35^{\circ}12'=$
35.2
$^{\circ}$,$18.375^{\circ}=$18
$^{\circ}$22
$'$30
$''$.答案:35.2
18
22
30
18
22
30
解析:
对于 $35^{\circ}12'$,由于$1^{\circ} = 60'$,所以$12'$可以转换为度数为 $\frac{12}{60} = 0.2^{\circ}$。
因此,$35^{\circ}12' = 35^{\circ} + 0.2^{\circ} = 35.2^{\circ}$。
对于 $18.375^{\circ}$,首先取整数部分得到$18^{\circ}$。
小数部分$0.375^{\circ}$转换为分,由于$1^{\circ} = 60'$,所以$0.375 × 60 = 22.5'$。
其中$22'$是整数部分,$0.5'$再转换为秒,由于$1' = 60''$,所以$0.5 × 60 = 30''$。
因此,$18.375^{\circ} = 18^{\circ}22'30''$。
因此,$35^{\circ}12' = 35^{\circ} + 0.2^{\circ} = 35.2^{\circ}$。
对于 $18.375^{\circ}$,首先取整数部分得到$18^{\circ}$。
小数部分$0.375^{\circ}$转换为分,由于$1^{\circ} = 60'$,所以$0.375 × 60 = 22.5'$。
其中$22'$是整数部分,$0.5'$再转换为秒,由于$1' = 60''$,所以$0.5 × 60 = 30''$。
因此,$18.375^{\circ} = 18^{\circ}22'30''$。
4. (1)图中共有多少个角?用字母分别表示出来.
(2)图中各角之间有怎样的和、差关系?(写出一种即可)
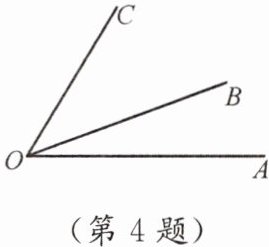
(2)图中各角之间有怎样的和、差关系?(写出一种即可)

答案:解:(1)3个,∠AOB,∠AOC,∠BOC
(2)∠AOB+∠BOC=∠AOC
(2)∠AOB+∠BOC=∠AOC
1. 已知$∠AOB= 100^{\circ}$,如果以O为顶点,OB为一边画$∠BOC= 20^{\circ}$,那么$∠AOC$的度数为(
A.$80^{\circ}$
B.$20^{\circ}$
C.$120^{\circ}$
D.$80^{\circ}或120^{\circ}$
D
)A.$80^{\circ}$
B.$20^{\circ}$
C.$120^{\circ}$
D.$80^{\circ}或120^{\circ}$
答案:D
解析:
当OC在∠AOB内部时,∠AOC=∠AOB - ∠BOC=100° - 20°=80°;
当OC在∠AOB外部时,∠AOC=∠AOB + ∠BOC=100° + 20°=120°;
∠AOC的度数为80°或120°。
D
当OC在∠AOB外部时,∠AOC=∠AOB + ∠BOC=100° + 20°=120°;
∠AOC的度数为80°或120°。
D
2. 利用一副三角板能画出一些特殊角度的角,下列角度不能用一副三角板画出的是 (
A.$105^{\circ}$
B.$15^{\circ}$
C.$175^{\circ}$
D.$135^{\circ}$
C
)A.$105^{\circ}$
B.$15^{\circ}$
C.$175^{\circ}$
D.$135^{\circ}$
答案:C
解析:
一副三角板的角度有$30^{\circ}$、$45^{\circ}$、$60^{\circ}$、$90^{\circ}$。
$105^{\circ}=60^{\circ}+45^{\circ}$,可画出;
$15^{\circ}=45^{\circ}-30^{\circ}$,可画出;
$135^{\circ}=90^{\circ}+45^{\circ}$,可画出;
$175^{\circ}$不能用上述角度的和或差表示。
C
$105^{\circ}=60^{\circ}+45^{\circ}$,可画出;
$15^{\circ}=45^{\circ}-30^{\circ}$,可画出;
$135^{\circ}=90^{\circ}+45^{\circ}$,可画出;
$175^{\circ}$不能用上述角度的和或差表示。
C
3. 如图,$∠BOD= ∠$
$∠AOD= ∠$

BOC
$+∠$COD
$=∠$AOD
$-∠$AOB
;$∠AOD= ∠$
AOB
$+∠$BOC
$+∠$COD
$=∠COD+∠$AOC
.
答案:BOC
COD
AOD
AOB
AOB
BOC
COD
AOC
COD
AOD
AOB
AOB
BOC
COD
AOC
解析:
由图可知:
$\angle BOD=\angle BOC+\angle COD=\angle AOD-\angle AOB$;
$\angle AOD=\angle AOB+\angle BOC+\angle COD=\angle COD+\angle AOC$。
$\angle BOD=\angle BOC+\angle COD=\angle AOD-\angle AOB$;
$\angle AOD=\angle AOB+\angle BOC+\angle COD=\angle COD+\angle AOC$。
4. 将一副三角板按图示方法放置(直角顶点重合),则$∠AOB+∠DOC=$
180
$^{\circ}$.答案:180
解析:
设$\angle AOD = \alpha$,
因为$\angle AOC = 90^\circ$,所以$\angle DOC = 90^\circ - \alpha$,
因为$\angle DOB = 90^\circ$,所以$\angle AOB = \angle AOD + \angle DOB = \alpha + 90^\circ$,
则$\angle AOB + \angle DOC = (\alpha + 90^\circ) + (90^\circ - \alpha) = 180^\circ$。
180
因为$\angle AOC = 90^\circ$,所以$\angle DOC = 90^\circ - \alpha$,
因为$\angle DOB = 90^\circ$,所以$\angle AOB = \angle AOD + \angle DOB = \alpha + 90^\circ$,
则$\angle AOB + \angle DOC = (\alpha + 90^\circ) + (90^\circ - \alpha) = 180^\circ$。
180
5. (1)你观察过钟面吗?钟面上的数从1到12,共有12个大格、60个小格,时针1h转过
(2)2时30分时,时针与分针所成的角为
(3)从3时15分到3时30分,时针转了
(4)时针从2时整的位置起,按顺时针方向转
30
$^{\circ}$,分针1min转过6
$^{\circ}$;(2)2时30分时,时针与分针所成的角为
105
$^{\circ}$;(3)从3时15分到3时30分,时针转了
7.5
$^{\circ}$,分针转了90
$^{\circ}$;(4)时针从2时整的位置起,按顺时针方向转
$\frac{60}{11}$
$^{\circ}$以后时针与分针重合.答案:30
6
105
7.5
90
$\frac{60}{11}$
6
105
7.5
90
$\frac{60}{11}$