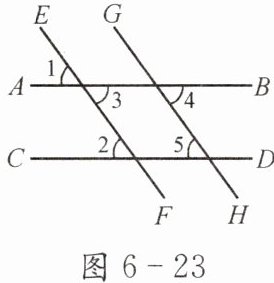
如图 6-23,直线 AB,CD 与直线 EF,GH 分别相交.
(1) 若∠1= ∠2,能得到哪两条直线平行?
(2) 若∠3= ∠4,能得到哪两条直线平行? 若∠2= ∠5 呢?
(1) 若∠1= ∠2,能得到哪两条直线平行?
(2) 若∠3= ∠4,能得到哪两条直线平行? 若∠2= ∠5 呢?

答案:(1)因为$\angle 1$和$\angle 2$是同位角,且$\angle 1 = \angle 2$,
根据同位角相等,两直线平行,
所以$AB// CD$。
(2)因为$\angle 3$和$\angle 4$是内错角,且$\angle 3 = \angle 4$,
根据内错角相等,两直线平行,
所以$EF// GH$。
因为$\angle 2$和$\angle 5$是同位角,且$\angle 2 = \angle 5$,
根据同位角相等,两直线平行,
所以$EF// GH$。
根据同位角相等,两直线平行,
所以$AB// CD$。
(2)因为$\angle 3$和$\angle 4$是内错角,且$\angle 3 = \angle 4$,
根据内错角相等,两直线平行,
所以$EF// GH$。
因为$\angle 2$和$\angle 5$是同位角,且$\angle 2 = \angle 5$,
根据同位角相等,两直线平行,
所以$EF// GH$。
1. 下列各图中,∠1 和∠2 为同位角的是

①②⑤
(填序号).
答案:①②⑤
2. 如图,若∠
C
= ∠1
,则 AC//ED,这是因为同位角相等,两直线平行
;若∠B
= ∠3
,则 AB//FD,这是因为同位角相等,两直线平行
.答案:C
1
同位角相等,两直线平行
B
3
同位角相等,两直线平行
1
同位角相等,两直线平行
B
3
同位角相等,两直线平行
解析:
若$\angle 1=\angle 3$,根据内错角相等,两直线平行,可得$AC// ED$;
若$\angle B=\angle FDE$,根据同位角相等,两直线平行,可得$AB// FD$。
若$\angle B=\angle FDE$,根据同位角相等,两直线平行,可得$AB// FD$。
3. 如图,在同一平面内,如果两条直线 b,c 都垂直于同一条直线 a,那么直线 b,c 互相平行吗?为什么?


答案:解:平行,因为a⊥b,a⊥c,所以∠1=∠2=90°,所以b//c
1. 如图,已知直线 AB,CD 分别与直线 EF 相交于点 M,N,且∠1= ∠2.
(1) 如果∠BMN= ∠DNF,那么 MQ//NP 是否成立? 请说明理由.
(2) 再添加一个条件:
(1) 如果∠BMN= ∠DNF,那么 MQ//NP 是否成立? 请说明理由.
解:(1)成立,因为∠BMN=∠DNF,又因为∠1=∠2,所以∠BMN+∠1=∠DNF+∠2,则∠PNF=∠QMN,所以MQ//NP
(2) 再添加一个条件:
∠EMB=∠END
,也可以得到 MQ//NP. 请说明理由.解:(2)∵∠EMB=∠END,∠1=∠2,∴∠EMQ=∠ENP,∴MQ//NP
答案:∠EMB=∠END
解:(1)成立,因为∠BMN=∠DNF,又因为∠1=∠2
所以∠BMN+∠1=∠DNF+∠2,则∠PNF=∠QM,所以MQ//NP
(2)∵∠EMB=∠END,∠1=∠2
∴∠EMQ=∠ENP,∴MQ//NP
解:(1)成立,因为∠BMN=∠DNF,又因为∠1=∠2
所以∠BMN+∠1=∠DNF+∠2,则∠PNF=∠QM,所以MQ//NP
(2)∵∠EMB=∠END,∠1=∠2
∴∠EMQ=∠ENP,∴MQ//NP
2. 如图,AB⊥BC,∠1+∠2= 90°,∠2= ∠3. 你能说明 BE//DF 吗?


答案:解:因为AB⊥BC,所以∠ABC=90°
即∠3+∠EBC=90°
因为∠1+∠2=90°,∠2=∠3
所以∠1=∠EBC,所以BE//DF
即∠3+∠EBC=90°
因为∠1+∠2=90°,∠2=∠3
所以∠1=∠EBC,所以BE//DF