如图 6-34,已知 AB//CD,试再添加一个条件,使∠1= ∠2,并说明你的理由.
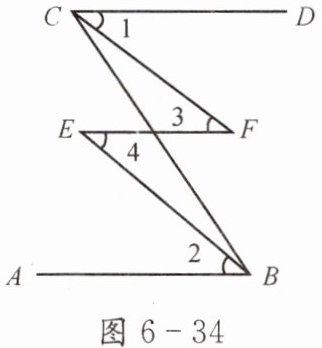

答案:第一种情况:添加条件为$EF// AB$。
理由:
因为$AB// CD$,$EF// AB$,根据平行公理的推论:平行于同一条直线的两条直线互相平行,所以$EF// CD$。
由两直线平行,内错角相等,可得$\angle 1=\angle 3$,$\angle 2=\angle 3$。
所以$\angle 1 = \angle 2$。
第二种情况:添加条件为$EF// CD$。
理由:
因为$AB// CD$,$EF// CD$,根据平行公理的推论:平行于同一条直线的两条直线互相平行,所以$EF// AB$。
由两直线平行,内错角相等,可得$\angle 1=\angle 3$,$\angle 2=\angle 3$。
所以$\angle 1 = \angle 2$。
第三种情况:添加条件为$\angle 3=\angle 4$。
理由:
因为$AB// CD$,根据两直线平行,内错角相等,所以$\angle 1=\angle 3$。
又因为$\angle 3=\angle 4$,$\angle 2=\angle 4$(对顶角相等),所以$\angle 1 = \angle 2$。
理由:
因为$AB// CD$,$EF// AB$,根据平行公理的推论:平行于同一条直线的两条直线互相平行,所以$EF// CD$。
由两直线平行,内错角相等,可得$\angle 1=\angle 3$,$\angle 2=\angle 3$。
所以$\angle 1 = \angle 2$。
第二种情况:添加条件为$EF// CD$。
理由:
因为$AB// CD$,$EF// CD$,根据平行公理的推论:平行于同一条直线的两条直线互相平行,所以$EF// AB$。
由两直线平行,内错角相等,可得$\angle 1=\angle 3$,$\angle 2=\angle 3$。
所以$\angle 1 = \angle 2$。
第三种情况:添加条件为$\angle 3=\angle 4$。
理由:
因为$AB// CD$,根据两直线平行,内错角相等,所以$\angle 1=\angle 3$。
又因为$\angle 3=\angle 4$,$\angle 2=\angle 4$(对顶角相等),所以$\angle 1 = \angle 2$。
1. 将一张五边形纸片剪去一个角,得到的一定是四边形吗?画出所有可能的图形.
答案:
答:不一定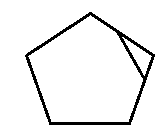
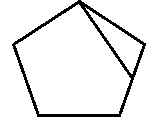
答:不一定


解析:
得到的不一定是四边形。
可能的图形有:
1. 四边形(沿一个角的两边剪去一个角);
2. 五边形(沿一个角的一边和另一边的延长线剪去一个角);
3. 六边形(沿相邻两边的延长线剪去一个角)。
(注:此处需根据实际图形绘制,文字描述仅为示意,实际答题时应画出三种图形。)
可能的图形有:
1. 四边形(沿一个角的两边剪去一个角);
2. 五边形(沿一个角的一边和另一边的延长线剪去一个角);
3. 六边形(沿相邻两边的延长线剪去一个角)。
(注:此处需根据实际图形绘制,文字描述仅为示意,实际答题时应画出三种图形。)
2. 如果将一张多边形纸片剪去一个角后得到一个四边形,那么原多边形的边数是多少?
答案:设原多边形的边数为$n$。
当剪去一个角后,多边形的边数可能增加$1$,可能减少$1$,也可能不变。
若边数增加$1$,则有$n + 1 = 4$,解得$n = 3$。
若边数减少$1$,则有$n - 1 = 4$,解得$n = 5$。
若边数不变,则有$n = 4$。
所以,原多边形的边数可以为$3$,$4$或$5$。
当剪去一个角后,多边形的边数可能增加$1$,可能减少$1$,也可能不变。
若边数增加$1$,则有$n + 1 = 4$,解得$n = 3$。
若边数减少$1$,则有$n - 1 = 4$,解得$n = 5$。
若边数不变,则有$n = 4$。
所以,原多边形的边数可以为$3$,$4$或$5$。
1. 将一张长方形纸片按如图所示的方式对折三次,产生的折痕之间的位置关系为(
A.平行
B.垂直
C.平行或垂直
D.无法确定
C
)A.平行
B.垂直
C.平行或垂直
D.无法确定
答案:C
解析:
第一次对折产生一条折痕;第二次对折方向与第一次相同,产生的折痕与第一条平行;第三次对折方向与前两次垂直,产生的折痕与前两条垂直。所以折痕之间的位置关系为平行或垂直。
C
C
2. 如图,从 A 地到 B 地有①②③三条路可以走,每条路长分别为 l,m,n,则(

A.l>m>n
B.l= m>n
C.m<n= l
D.l<m<n
B
)
A.l>m>n
B.l= m>n
C.m<n= l
D.l<m<n
答案:B
解析:
观察图形,路线①是水平和竖直方向的折线,其长度等于长方形的一条长与一条宽之和;路线③同样是水平和竖直方向的折线,长度也等于长方形的一条长与一条宽之和,所以$l = n$。路线②是连接A、B两地的斜线,根据“两点之间,线段最短”,斜线长度小于折线长度,即$m < l$(或$m < n$)。综上可得$m < n = l$。
C
C