3. 如图,将长方形纸片的一角斜折过去,使角的顶点 A 落在点 F 处,BC 为折痕,BD 为∠EBF 的平分线,则∠CBD=
90
°.答案:90
解析:
由折叠性质得∠ABC=∠FBC。
∵BD为∠EBF的平分线,
∴∠FBD=∠EBD。
∵∠ABC+∠FBC+∠FBD+∠EBD=180°,
∴2∠FBC+2∠FBD=180°,
∴∠FBC+∠FBD=90°,即∠CBD=90°。
90
∵BD为∠EBF的平分线,
∴∠FBD=∠EBD。
∵∠ABC+∠FBC+∠FBD+∠EBD=180°,
∴2∠FBC+2∠FBD=180°,
∴∠FBC+∠FBD=90°,即∠CBD=90°。
90
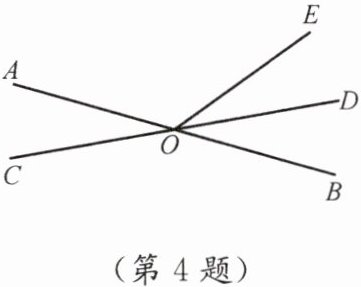
4. 如图,直线 AB,CD 相交于点 O,OE 是射线,OD 是∠BOE 的平分线,且∠BOE= $\frac{2}{5}$∠AOE,求∠AOC 的大小.

答案:解:
1. 设$\angle BOE = 2x$,因为$\angle BOE=\frac{2}{5}\angle AOE$,所以$\angle AOE = 5x$。
由于$\angle AOE+\angle BOE = 180^{\circ}$(邻补角的定义),即$5x + 2x=180^{\circ}$。
合并同类项得$7x = 180^{\circ}$,解得$x=\frac{180^{\circ}}{7}$。
2. 因为$OD$是$\angle BOE$的平分线,所以$\angle BOD=\frac{1}{2}\angle BOE$。
把$\angle BOE = 2x$代入,得$\angle BOD=x$。
3. 又因为$\angle AOC$与$\angle BOD$是对顶角(对顶角的定义)。
根据对顶角相等,$\angle AOC=\angle BOD$。
把$x = \frac{180^{\circ}}{7}$代入,得$\angle AOC=\frac{180^{\circ}}{7}\approx25.71^{\circ}$。
综上,$\angle AOC$的大小为$\frac{180^{\circ}}{7}$。
1. 设$\angle BOE = 2x$,因为$\angle BOE=\frac{2}{5}\angle AOE$,所以$\angle AOE = 5x$。
由于$\angle AOE+\angle BOE = 180^{\circ}$(邻补角的定义),即$5x + 2x=180^{\circ}$。
合并同类项得$7x = 180^{\circ}$,解得$x=\frac{180^{\circ}}{7}$。
2. 因为$OD$是$\angle BOE$的平分线,所以$\angle BOD=\frac{1}{2}\angle BOE$。
把$\angle BOE = 2x$代入,得$\angle BOD=x$。
3. 又因为$\angle AOC$与$\angle BOD$是对顶角(对顶角的定义)。
根据对顶角相等,$\angle AOC=\angle BOD$。
把$x = \frac{180^{\circ}}{7}$代入,得$\angle AOC=\frac{180^{\circ}}{7}\approx25.71^{\circ}$。
综上,$\angle AOC$的大小为$\frac{180^{\circ}}{7}$。
5. 如图,在六边形 ABCDEF 中,AF//CD,∠A= 140°,∠C= 165°.
(1)求∠B 的度数;
(2)要使 AB//DE,∠D 的大小应为

(1)
(1)求∠B 的度数;
(2)要使 AB//DE,∠D 的大小应为
140°
.
(1)
过点B作BG//AF,
∵AF//CD,∴BG//CD(平行于同一直线的两直线平行)。
∵AF//BG,∴∠A+∠ABG=180°(两直线平行,同旁内角互补),
∵∠A=140°,∴∠ABG=180°-140°=40°。
∵BG//CD,∴∠CBG+∠C=180°(两直线平行,同旁内角互补),
∵∠C=165°,∴∠CBG=180°-165°=15°。
∴∠B=∠ABG+∠CBG=40°+15°=55°。
∵AF//CD,∴BG//CD(平行于同一直线的两直线平行)。
∵AF//BG,∴∠A+∠ABG=180°(两直线平行,同旁内角互补),
∵∠A=140°,∴∠ABG=180°-140°=40°。
∵BG//CD,∴∠CBG+∠C=180°(两直线平行,同旁内角互补),
∵∠C=165°,∴∠CBG=180°-165°=15°。
∴∠B=∠ABG+∠CBG=40°+15°=55°。
答案:(1)过点B作BG//AF,
∵AF//CD,∴BG//CD(平行于同一直线的两直线平行)。
∵AF//BG,∴∠A+∠ABG=180°(两直线平行,同旁内角互补),
∵∠A=140°,∴∠ABG=180°-140°=40°。
∵BG//CD,∴∠CBG+∠C=180°(两直线平行,同旁内角互补),
∵∠C=165°,∴∠CBG=180°-165°=15°。
∴∠B=∠ABG+∠CBG=40°+15°=55°。
(2)140°
∵AF//CD,∴BG//CD(平行于同一直线的两直线平行)。
∵AF//BG,∴∠A+∠ABG=180°(两直线平行,同旁内角互补),
∵∠A=140°,∴∠ABG=180°-140°=40°。
∵BG//CD,∴∠CBG+∠C=180°(两直线平行,同旁内角互补),
∵∠C=165°,∴∠CBG=180°-165°=15°。
∴∠B=∠ABG+∠CBG=40°+15°=55°。
(2)140°