1. 已知$x= 2是关于x的方程2x+k-1= 0$的解,则$k= $
-3
.答案:-3
解析:
将$x = 2$代入方程$2x + k - 1 = 0$,得$2×2 + k - 1 = 0$,即$4 + k - 1 = 0$,$3 + k = 0$,解得$k=-3$。
$-3$
$-3$
2. 若代数式$1-\frac{3-y}{2}$的值为-1,则$y=$
-1
.答案:-1
解析:
由题意得:$1 - \frac{3 - y}{2} = -1$
两边同乘2:$2 - (3 - y) = -2$
去括号:$2 - 3 + y = -2$
合并同类项:$-1 + y = -2$
移项:$y = -2 + 1$
解得:$y = -1$
$-1$
两边同乘2:$2 - (3 - y) = -2$
去括号:$2 - 3 + y = -2$
合并同类项:$-1 + y = -2$
移项:$y = -2 + 1$
解得:$y = -1$
$-1$
3. 小华在解方程$5x-1= ( )x+3$时,把“( )”处的数字看成了它的相反数,解得$x= 2$,则该方程的正确解应为$x= $
$\frac {1}{2}$
.答案:
$\frac {1}{2}$
$\frac {1}{2}$
解析:
设“( )”处的数字为$a$,则小华看成了$-a$。
将$x = 2$代入$5x - 1=-ax + 3$,得:
$5×2 - 1=-a×2 + 3$
$10 - 1=-2a + 3$
$9=-2a + 3$
$-2a=6$
$a=-3$
原方程为$5x - 1=-3x + 3$
$5x + 3x=3 + 1$
$8x=4$
$x=\frac{4}{8}=\frac{1}{2}$
$\frac{1}{2}$
将$x = 2$代入$5x - 1=-ax + 3$,得:
$5×2 - 1=-a×2 + 3$
$10 - 1=-2a + 3$
$9=-2a + 3$
$-2a=6$
$a=-3$
原方程为$5x - 1=-3x + 3$
$5x + 3x=3 + 1$
$8x=4$
$x=\frac{4}{8}=\frac{1}{2}$
$\frac{1}{2}$
4. 小刚今年6岁,他的爷爷72岁.
16
年后,小刚的年龄是爷爷的$\frac{1}{4}$.答案:16
解析:
设$x$年后,小刚的年龄是爷爷的$\frac{1}{4}$。
根据题意,得$6 + x = \frac{1}{4}(72 + x)$。
解方程:
$4(6 + x) = 72 + x$
$24 + 4x = 72 + x$
$4x - x = 72 - 24$
$3x = 48$
$x = 16$。
16
根据题意,得$6 + x = \frac{1}{4}(72 + x)$。
解方程:
$4(6 + x) = 72 + x$
$24 + 4x = 72 + x$
$4x - x = 72 - 24$
$3x = 48$
$x = 16$。
16
5. 写出一个解为$x= 1$的一元一次方程,要求至少含有一个分母和一个括号:
$\frac {3(x+1)}{4}-\frac {1}{2}=1$
.答案:$\frac {3(x+1)}{4}-\frac {1}{2}=1$
6. 如图,将同样大小的棋子按规律摆放,若第$n$个图中有2022枚棋子,则$n= $
673
.答案:673
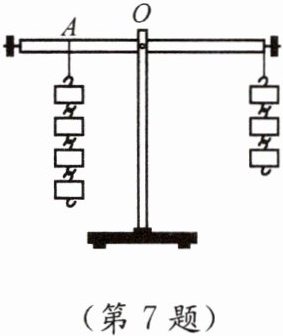
7. 根据杠杆原理,要使杠杆平衡,则作用在杠杆上的两个力矩(力与力臂的乘积)大小必须相等.如图,杠杆左边挂了4个砝码,右边挂了3个砝码,这些砝码质量相同,且杠杆保持平衡.设木杆长$a\ cm$,支点在木杆的中点处,左边的力臂(支点$O到木杆左边挂砝码处点A$的距离)为$x\ cm$,把$a$作为已知数,根据题意,列出关于$x$的一元一次方程为______.

$ 4x=3×\frac {1}{2}a$
答案:
$ 4x=3×\frac {1}{2}a$
$ 4x=3×\frac {1}{2}a$
解析:
设砝码质量为$m$。
左边力矩为$4× m× x$;
右边力臂为$(a/2-x)$,
右边力矩为$3× m×(a/2-x)$。
根据杠杆平衡条件,左边力矩等于右边力矩,
可得方程:$4mx=3m(\frac{a}{2}-x)$。
两边同时除以$m$,
得$4x=3(\frac{a}{2}-x)$。
左边力矩为$4× m× x$;
右边力臂为$(a/2-x)$,
右边力矩为$3× m×(a/2-x)$。
根据杠杆平衡条件,左边力矩等于右边力矩,
可得方程:$4mx=3m(\frac{a}{2}-x)$。
两边同时除以$m$,
得$4x=3(\frac{a}{2}-x)$。
8. 规定$m\triangle n= 3m-2n$,已知$x\triangle(8\triangle4)= 40$,那么$x= $
24
.答案:24
解析:
先计算$8\triangle4$:
$8\triangle4 = 3×8 - 2×4 = 24 - 8 = 16$
则$x\triangle16 = 40$,即:
$3x - 2×16 = 40$
$3x - 32 = 40$
$3x = 40 + 32$
$3x = 72$
$x = 24$
24
$8\triangle4 = 3×8 - 2×4 = 24 - 8 = 16$
则$x\triangle16 = 40$,即:
$3x - 2×16 = 40$
$3x - 32 = 40$
$3x = 40 + 32$
$3x = 72$
$x = 24$
24
9. 下列各式进行的变形中,不正确的是(
A.若$3a= 2b$,则$3a+2= 2b+2$
B.若$3a= 2b$,则$9a= 4b$
C.若$3a= 2b$,则$3a-5= 2b-5$
D.若$3a= 2b$,则$\frac{a}{2}= \frac{b}{3}$
B
)A.若$3a= 2b$,则$3a+2= 2b+2$
B.若$3a= 2b$,则$9a= 4b$
C.若$3a= 2b$,则$3a-5= 2b-5$
D.若$3a= 2b$,则$\frac{a}{2}= \frac{b}{3}$
答案:B
解析:
A. 若$3a = 2b$,等式两边同时加2,得$3a + 2 = 2b + 2$,变形正确;
B. 若$3a = 2b$,等式两边同时乘3,得$9a = 6b$,原变形$9a = 4b$不正确;
C. 若$3a = 2b$,等式两边同时减5,得$3a - 5 = 2b - 5$,变形正确;
D. 若$3a = 2b$,等式两边同时除以6,得$\frac{a}{2} = \frac{b}{3}$,变形正确。
B
B. 若$3a = 2b$,等式两边同时乘3,得$9a = 6b$,原变形$9a = 4b$不正确;
C. 若$3a = 2b$,等式两边同时减5,得$3a - 5 = 2b - 5$,变形正确;
D. 若$3a = 2b$,等式两边同时除以6,得$\frac{a}{2} = \frac{b}{3}$,变形正确。
B
10. 方程$x^{2}= 1$,$y= x+2$,$\frac{x}{2}= x-3$,$\frac{1}{x-2}= 1$,$2(x-3)= 0$中,是一元一次方程的有(
A.1个
B.2个
C.3个
D.4个
B
)A.1个
B.2个
C.3个
D.4个
答案:B
解析:
$x^{2}=1$:未知数最高次数为2,不是一元一次方程;
$y=x+2$:含有两个未知数,不是一元一次方程;
$\frac{x}{2}=x-3$:只含一个未知数,未知数最高次数为1,是一元一次方程;
$\frac{1}{x-2}=1$:分母含未知数,不是整式方程,不是一元一次方程;
$2(x-3)=0$:只含一个未知数,未知数最高次数为1,是一元一次方程;
是一元一次方程的有2个。
B
$y=x+2$:含有两个未知数,不是一元一次方程;
$\frac{x}{2}=x-3$:只含一个未知数,未知数最高次数为1,是一元一次方程;
$\frac{1}{x-2}=1$:分母含未知数,不是整式方程,不是一元一次方程;
$2(x-3)=0$:只含一个未知数,未知数最高次数为1,是一元一次方程;
是一元一次方程的有2个。
B
11. 我国古代数学名著中有一道题“以绳测井”问题。用绳子量井深,把绳3折来量,井外余绳4尺;把绳4折来量,井外余绳1尺.绳长、井深各几尺? 若设绳长为$x$尺,则下面所列方程正确的是(
A.$3(x-1)= 4(x-4)$
B.$3(x+4)= 4(x+1)$
C.$\frac{1}{4}x-4= \frac{1}{3}x-1$
D.$\frac{1}{3}x-4= \frac{1}{4}x-1$
D
)A.$3(x-1)= 4(x-4)$
B.$3(x+4)= 4(x+1)$
C.$\frac{1}{4}x-4= \frac{1}{3}x-1$
D.$\frac{1}{3}x-4= \frac{1}{4}x-1$
答案:D
解析:
设绳长为$x$尺,井深为$y$尺。
把绳3折来量,井外余绳4尺,可得井深$y = \frac{1}{3}x - 4$;
把绳4折来量,井外余绳1尺,可得井深$y = \frac{1}{4}x - 1$。
因为井深不变,所以$\frac{1}{3}x - 4 = \frac{1}{4}x - 1$。
D
把绳3折来量,井外余绳4尺,可得井深$y = \frac{1}{3}x - 4$;
把绳4折来量,井外余绳1尺,可得井深$y = \frac{1}{4}x - 1$。
因为井深不变,所以$\frac{1}{3}x - 4 = \frac{1}{4}x - 1$。
D