4.(1)$-2$的绝对值是
(2)绝对值不大于3的非负整数是
2
,$\frac{2}{3}$的绝对值是$\frac{2}{3}$
,绝对值等于3的数是±3
;(2)绝对值不大于3的非负整数是
0,1,2,3
.答案:2
$\frac{2}{3}$
±3
0,1,2,3
$\frac{2}{3}$
±3
0,1,2,3
解析:
(1)根据绝对值的定义,负数的绝对值是它的相反数,正数的绝对值是它本身,0的绝对值是0。所以-2的绝对值是2,$\frac{2}{3}$的绝对值是$\frac{2}{3}$;绝对值等于3的数是±3。
(2)绝对值不大于3即绝对值小于或等于3,非负整数包括0和正整数,所以符合条件的数是0,1,2,3。
(2)绝对值不大于3即绝对值小于或等于3,非负整数包括0和正整数,所以符合条件的数是0,1,2,3。
5. 已知$|a|= \left|-\frac{1}{2}\right|$,那么$a$的值是
$±\frac{1}{2}$
.答案:$±\frac{1}{2}$
解析:
因为$\left|-\frac{1}{2}\right| = \frac{1}{2}$,所以$|a| = \frac{1}{2}$。根据绝对值的定义,绝对值等于$\frac{1}{2}$的数有两个,即$a = \frac{1}{2}$或$a = -\frac{1}{2}$。
6. 用“>”“<”或“=”填空:
(1)$-1$
(2)$-|-2|$
(3)$-0.3$
(4)$-\left(-\frac{1}{9}\right)$
(1)$-1$
<
$-0.01$;(2)$-|-2|$
<
0;(3)$-0.3$
>
$-\frac{1}{3}$;(4)$-\left(-\frac{1}{9}\right)$
>
$-\left|-\frac{1}{10}\right|$.答案:<
<
>
>
<
>
>
解析:
(1) 对于$-1$和$-0.01$,由于它们都是负数,且$|-1| > |-0.01|$,根据负数的性质,绝对值大的负数反而小,所以$-1 < -0.01$。
(2) 对于$-|-2|$,首先计算绝对值$|-2| = 2$,再取负得$-2$。显然,$-2 < 0$,所以$-|-2| < 0$。
(3) 对于$-0.3$和$-\frac{1}{3}$,首先将它们转换为相同的数制以便比较。$-0.3 = -\frac{3}{10}$,而$-\frac{1}{3} = -\frac{10}{30}$。由于$\frac{3}{10} < \frac{10}{30}$,根据负数的性质,绝对值大的负数反而小,所以$-0.3 > -\frac{1}{3}$。
(4) 对于$-\left(-\frac{1}{9}\right)$和$-\left|-\frac{1}{10}\right|$,首先计算各自的数值。$-\left(-\frac{1}{9}\right) = \frac{1}{9}$,而$-\left|-\frac{1}{10}\right| = -\frac{1}{10}$。显然,正数大于负数,所以$-\left(-\frac{1}{9}\right) > -\left|-\frac{1}{10}\right|$。
(2) 对于$-|-2|$,首先计算绝对值$|-2| = 2$,再取负得$-2$。显然,$-2 < 0$,所以$-|-2| < 0$。
(3) 对于$-0.3$和$-\frac{1}{3}$,首先将它们转换为相同的数制以便比较。$-0.3 = -\frac{3}{10}$,而$-\frac{1}{3} = -\frac{10}{30}$。由于$\frac{3}{10} < \frac{10}{30}$,根据负数的性质,绝对值大的负数反而小,所以$-0.3 > -\frac{1}{3}$。
(4) 对于$-\left(-\frac{1}{9}\right)$和$-\left|-\frac{1}{10}\right|$,首先计算各自的数值。$-\left(-\frac{1}{9}\right) = \frac{1}{9}$,而$-\left|-\frac{1}{10}\right| = -\frac{1}{10}$。显然,正数大于负数,所以$-\left(-\frac{1}{9}\right) > -\left|-\frac{1}{10}\right|$。
1. 若$|a-2|+|b-7|= 0$,则$b-a= $
5
.答案:5
解析:
因为$|a - 2| + |b - 7| = 0$,且绝对值具有非负性,所以$|a - 2| = 0$,$|b - 7| = 0$。
由$|a - 2| = 0$可得$a - 2 = 0$,解得$a = 2$;
由$|b - 7| = 0$可得$b - 7 = 0$,解得$b = 7$。
则$b - a = 7 - 2 = 5$。
5
由$|a - 2| = 0$可得$a - 2 = 0$,解得$a = 2$;
由$|b - 7| = 0$可得$b - 7 = 0$,解得$b = 7$。
则$b - a = 7 - 2 = 5$。
5
2. 如图,四个有理数在数轴上的对应点分别为$M$,$P$,$N$,$Q$.若点$M$,$N$表示的有理数互为相反数,则点$M$,$P$,$N$,$Q$中,表示的数的绝对值最小的点是
P
.答案:P
解析:
由于点$M$和点$N$表示的有理数互为相反数,根据相反数的定义,它们在数轴上关于原点对称。
因此,原点$O$是$M$和$N$的中点。
从数轴上看,点$P$离原点$O$最近。
根据绝对值的定义,一个数的绝对值就是它到原点的距离。
所以,点$P$表示的数的绝对值最小。
因此,原点$O$是$M$和$N$的中点。
从数轴上看,点$P$离原点$O$最近。
根据绝对值的定义,一个数的绝对值就是它到原点的距离。
所以,点$P$表示的数的绝对值最小。
3. 我们知道,对于有理数$a$,当$a>0$时,$|a|= a$;当$a<0$时,$|a|= -a$;当$a= 0$时,$|a|= a$.由此可知,对于$a-b$,若$a>b$,则$a-b>0$,即$|a-b|= a-b$;若$a<b$,则$a-b<0$,即$|a-b|= b-a$;若$a= b$,则$a-b= 0$,即$|a-b|= 0$.据此回答问题:
(1)在$|x-1|$中,当$x>1$时,$x-1$
(2)在$|x-1|$中,当$x<1$时,$x-1$
(3)在$|x-1|$中,当$x= 1$时,$x-1$
(4)数$a$,$b$,$c$在数轴上表示的点如图所示,则$|b-a|= $
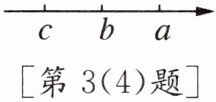
(1)在$|x-1|$中,当$x>1$时,$x-1$
>
0,$|x-1|= $x-1
;(2)在$|x-1|$中,当$x<1$时,$x-1$
<
0,$|x-1|= $1-x
;(3)在$|x-1|$中,当$x= 1$时,$x-1$
=
0,$|x-1|= $0
;(4)数$a$,$b$,$c$在数轴上表示的点如图所示,则$|b-a|= $
a-b
,$|b-c|= $b-c
.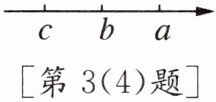
答案:
>
x-1
<
1-x
=
0
a-b
b-c
>
x-1
<
1-x
=
0
a-b
b-c
解析:
(1)当$x>1$时,$x-1>0$,根据绝对值的定义,正数的绝对值是它本身,所以$|x-1|=x-1$。
(2)当$x<1$时,$x-1<0$,根据绝对值的定义,负数的绝对值是它的相反数,所以$|x-1|=-(x-1)=1-x$。
(3)当$x=1$时,$x-1=0$,根据绝对值的定义,$0$的绝对值是$0$,所以$|x-1|=0$。
(4)由数轴可知$a>b>c$,那么$b-a<0$,根据绝对值的定义,负数的绝对值是它的相反数,所以$|b-a|=-(b-a)=a-b$;$b-c>0$,根据绝对值的定义,正数的绝对值是它本身,所以$|b-c|=b-c$。
(2)当$x<1$时,$x-1<0$,根据绝对值的定义,负数的绝对值是它的相反数,所以$|x-1|=-(x-1)=1-x$。
(3)当$x=1$时,$x-1=0$,根据绝对值的定义,$0$的绝对值是$0$,所以$|x-1|=0$。
(4)由数轴可知$a>b>c$,那么$b-a<0$,根据绝对值的定义,负数的绝对值是它的相反数,所以$|b-a|=-(b-a)=a-b$;$b-c>0$,根据绝对值的定义,正数的绝对值是它本身,所以$|b-c|=b-c$。
4. 请阅读材料,并解决问题.
在比较$-\frac{99}{201}与-\frac{51}{101}$的大小时,若利用绝对值法比较,则需要进行分数的通分,因为分母较大,所以比较烦琐.我们也可以使用如下的方法比较大小:
因为$\frac{99}{201}<\frac{1}{2}$,$\frac{51}{101}>\frac{1}{2}$,所以$\frac{99}{201}<\frac{51}{101}$,所以$-\frac{99}{201}>-\frac{51}{101}$.
(1)填空:上述方法是先通过找中间量
(2)利用上述方法比较$-\frac{43}{126}与-\frac{79}{243}$的大小.
解:因为$\frac{43}{126}>\frac{1}{3},\frac{79}{243}<\frac{1}{3}$
所以$\frac{43}{126}>\frac{79}{243}$
所以$-\frac{43}{126}<-\frac{79}{243}$
在比较$-\frac{99}{201}与-\frac{51}{101}$的大小时,若利用绝对值法比较,则需要进行分数的通分,因为分母较大,所以比较烦琐.我们也可以使用如下的方法比较大小:
因为$\frac{99}{201}<\frac{1}{2}$,$\frac{51}{101}>\frac{1}{2}$,所以$\frac{99}{201}<\frac{51}{101}$,所以$-\frac{99}{201}>-\frac{51}{101}$.
(1)填空:上述方法是先通过找中间量
$\frac{1}{2}$
来比较正数$\frac{99}{201}与\frac{51}{101}$的大小,再根据两个负数比较大小的结论“绝对值
大的负数反而小”进行判断.(2)利用上述方法比较$-\frac{43}{126}与-\frac{79}{243}$的大小.
解:因为$\frac{43}{126}>\frac{1}{3},\frac{79}{243}<\frac{1}{3}$
所以$\frac{43}{126}>\frac{79}{243}$
所以$-\frac{43}{126}<-\frac{79}{243}$
答案:$\frac{1}{2}$
绝对值
解$:-\frac{43}{126}<-\frac{79}{243}$
因为$\frac{43}{126}>\frac{1}{3},\frac{79}{243}<\frac{1}{3}$
所以$\frac{43}{126}>\frac{79}{243}$
所以$-\frac{43}{126}<-\frac{79}{243}$
绝对值
解$:-\frac{43}{126}<-\frac{79}{243}$
因为$\frac{43}{126}>\frac{1}{3},\frac{79}{243}<\frac{1}{3}$
所以$\frac{43}{126}>\frac{79}{243}$
所以$-\frac{43}{126}<-\frac{79}{243}$