写出等式的性质:
等式的两边加上或减去同一个数或相同的整式,等式仍然成立;等式的两边同时乘以或除以同一个不为零的数,等式仍然成立。
答案:等式的两边加上或减去同一个数或相同的整式,等式仍然成立;等式的两边同时乘以或除以同一个不为零的数,等式仍然成立。
解析:
等式具有两个重要的性质。首先,等式的两边加上或减去同一个数或相同的整式,等式仍然成立。其次,等式的两边同时乘以或除以同一个不为零的数,等式也仍然成立。
1. 观察下列方程的变形过程,并概括变形前后方程的变化.
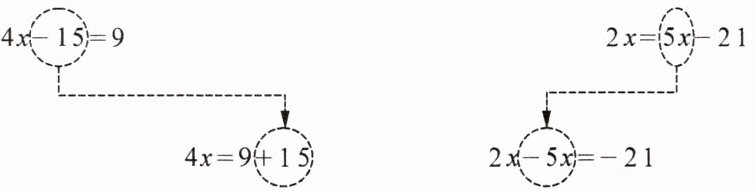
2. 什么是移项?移项的依据是什么?

2. 什么是移项?移项的依据是什么?
答案:解:方程两边同时加减同一个数或式子,依据是等式的基本性质
解:等式两边同加15
解:等式两边同减5x
解:等式两边同加15
解:等式两边同减5x
1. 尝试用移项的方法解方程:6-5x= 3x+22.
答案:解: 6-5x-3x-6=3x+22-3x-6
-8x÷(-8)=16÷(-8)
x=-2
解:移项的目的是将同类项移到等式的同一侧,通常把含未知数的项移到等式的一边,
常数项移到等式的另一边.移项时切记要变号
-8x÷(-8)=16÷(-8)
x=-2
解:移项的目的是将同类项移到等式的同一侧,通常把含未知数的项移到等式的一边,
常数项移到等式的另一边.移项时切记要变号
1. 解方程5x+2= 3时,下列移项中,正确的是 (
A.5x= 3+2
B.5x= -3-2
C.2+3= -5x
D.5x= 3-2
D
)A.5x= 3+2
B.5x= -3-2
C.2+3= -5x
D.5x= 3-2
答案:D
解析:
解方程$5x + 2 = 3$,移项得$5x = 3 - 2$,正确选项为D。
2. 如果代数式2x-1与4x+3的值相等,那么 (
A.x= 2
B.x= -2
C.$x= \frac{1}{2}$
D.$x= -\frac{1}{2}$
B
)A.x= 2
B.x= -2
C.$x= \frac{1}{2}$
D.$x= -\frac{1}{2}$
答案:B
解析:
2x-1=4x+3
2x-4x=3+1
-2x=4
x=-2
B
2x-4x=3+1
-2x=4
x=-2
B
3. 解下列方程:
(1)-3-3x= 2;
(2)15-x= 2x;
(3)$\frac{4}{3}x-16= -1$;
(4)$3x+\frac{1}{3}= 5x+\frac{1}{5}$;
(5)7x= 6x+12;
(6)3x-7= -x-1.
(1)-3-3x= 2;
(2)15-x= 2x;
(3)$\frac{4}{3}x-16= -1$;
(4)$3x+\frac{1}{3}= 5x+\frac{1}{5}$;
(5)7x= 6x+12;
(6)3x-7= -x-1.
答案:
(1)
解:-3 - 3x = 2
移项得:-3x = 2 + 3
合并同类项得:-3x = 5
系数化为1得:x = -$\frac{5}{3}$
(2)
解:15 - x = 2x
移项得:-x - 2x = -15
合并同类项得:-3x = -15
系数化为1得:x = 5
(3)
解:$\frac{4}{3}$x - 16 = -1
移项得:$\frac{4}{3}$x = -1 + 16
合并同类项得:$\frac{4}{3}$x = 15
系数化为1得:x = $\frac{45}{4}$
(4)
解:3x + $\frac{1}{3}$ = 5x + $\frac{1}{5}$
移项得:3x - 5x = $\frac{1}{5}$ - $\frac{1}{3}$
合并同类项得:-2x = -$\frac{2}{15}$
系数化为1得:x = $\frac{1}{15}$
(5)
解:7x = 6x + 12
移项得:7x - 6x = 12
合并同类项得:x = 12
(6)
解:3x - 7 = -x - 1
移项得:3x + x = -1 + 7
合并同类项得:4x = 6
系数化为1得:x = $\frac{3}{2}$
(1)
解:-3 - 3x = 2
移项得:-3x = 2 + 3
合并同类项得:-3x = 5
系数化为1得:x = -$\frac{5}{3}$
(2)
解:15 - x = 2x
移项得:-x - 2x = -15
合并同类项得:-3x = -15
系数化为1得:x = 5
(3)
解:$\frac{4}{3}$x - 16 = -1
移项得:$\frac{4}{3}$x = -1 + 16
合并同类项得:$\frac{4}{3}$x = 15
系数化为1得:x = $\frac{45}{4}$
(4)
解:3x + $\frac{1}{3}$ = 5x + $\frac{1}{5}$
移项得:3x - 5x = $\frac{1}{5}$ - $\frac{1}{3}$
合并同类项得:-2x = -$\frac{2}{15}$
系数化为1得:x = $\frac{1}{15}$
(5)
解:7x = 6x + 12
移项得:7x - 6x = 12
合并同类项得:x = 12
(6)
解:3x - 7 = -x - 1
移项得:3x + x = -1 + 7
合并同类项得:4x = 6
系数化为1得:x = $\frac{3}{2}$