1. 下列各图中,属于棱柱的有 (
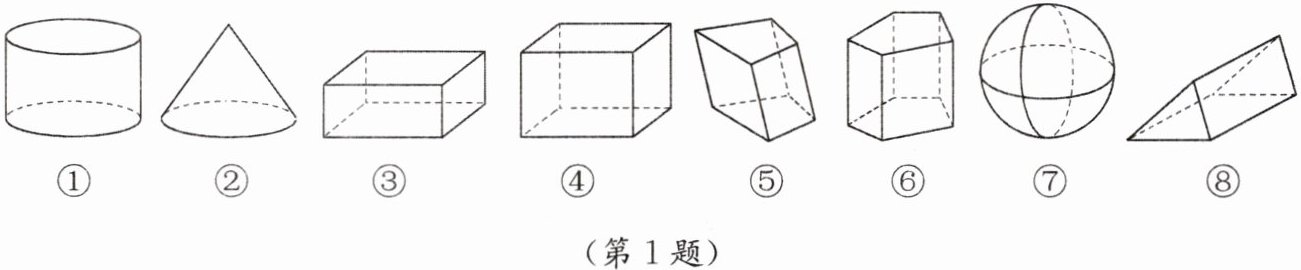
A.3个
B.4个
C.5个
D.6个
C
)
A.3个
B.4个
C.5个
D.6个
答案:C
解析:
棱柱的上下底面是全等的多边形,侧面是长方形。
图①是圆柱,不符合棱柱特征。
图②是圆锥,不符合棱柱特征。
图③是四棱柱,符合棱柱特征。
图④是正方体,属于棱柱。
图⑤是三棱柱,符合棱柱特征。
图⑥是五棱柱,符合棱柱特征。
图⑦是球体,不符合棱柱特征。
图⑧上下底面大小不同,不符合棱柱特征。
所以③④⑤⑥是棱柱,共4个。
图①是圆柱,不符合棱柱特征。
图②是圆锥,不符合棱柱特征。
图③是四棱柱,符合棱柱特征。
图④是正方体,属于棱柱。
图⑤是三棱柱,符合棱柱特征。
图⑥是五棱柱,符合棱柱特征。
图⑦是球体,不符合棱柱特征。
图⑧上下底面大小不同,不符合棱柱特征。
所以③④⑤⑥是棱柱,共4个。
2. 不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征. 甲同学说:“它有4个面是三角形.”乙同学说:“它有8条棱.”该几何体可能是 (
A.三棱柱
B.四棱柱
C.三棱锥
D.四棱锥
D
)A.三棱柱
B.四棱柱
C.三棱锥
D.四棱锥
答案:D
解析:
- 三棱柱:2个三角形面,3个矩形面,9条棱,不符合。
四棱柱:6个面均为四边形,12条棱,不符合。
三棱锥:4个三角形面,6条棱,不符合。
四棱锥:4个三角形侧面,1个四边形底面,8条棱,符合。
D
四棱柱:6个面均为四边形,12条棱,不符合。
三棱锥:4个三角形面,6条棱,不符合。
四棱锥:4个三角形侧面,1个四边形底面,8条棱,符合。
D
3. 将下列实物与相应的几何体用线连接起来.
篮球 现代汉语词典 一堆小麦 魔方 易拉罐
圆柱 圆锥 正方体 长方体 球
篮球 现代汉语词典 一堆小麦 魔方 易拉罐
圆柱 圆锥 正方体 长方体 球
答案:


解析:
首先,我们逐一分析每种实物与对应的几何体:
1. 篮球的形状是一个典型的球体,所以与“球”相连。
2. 现代汉语词典是一个较为规则的长方形状,因此与“长方体”相连。
3. 一堆小麦的形状呈圆锥状,所以与“圆锥”相连。
4. 魔方是一个正方体,每个面都是正方形,因此与“正方体”相连。
5. 易拉罐的形状是一个圆柱体,所以与“圆柱”相连。
根据以上分析,我们可以得出以下连线结果。
1. 篮球的形状是一个典型的球体,所以与“球”相连。
2. 现代汉语词典是一个较为规则的长方形状,因此与“长方体”相连。
3. 一堆小麦的形状呈圆锥状,所以与“圆锥”相连。
4. 魔方是一个正方体,每个面都是正方形,因此与“正方体”相连。
5. 易拉罐的形状是一个圆柱体,所以与“圆柱”相连。
根据以上分析,我们可以得出以下连线结果。
1. 下列图形中,不是立体图形的是 (
A.球
B.圆柱
C.圆锥
D.圆
D
)A.球
B.圆柱
C.圆锥
D.圆
答案:D
解析:
立体图形是指具有三维空间(长度、宽度和高度)的图形。球、圆柱和圆锥都占据三维空间,而圆只占据二维平面,不具有高度,因此不是立体图形。
2. 三棱锥有
6
条棱,四棱锥有8
条棱,五棱锥有10
条棱,n棱锥有2n
条棱,三十
棱锥有60条棱,十
棱柱有30条棱.答案:6
8
10
2n
三十
十
8
10
2n
三十
十
解析:
三棱锥:底面是三角形,有3条边,加上3条侧棱,共有$3+3=6$条棱。
四棱锥:底面是四边形,有4条边,加上4条侧棱,共有$4+4=8$条棱。
五棱锥:底面是五边形,有5条边,加上5条侧棱,共有$5+5=10$条棱。
n棱锥:底面是n边形,有n条边,加上n条侧棱,共有$n+n=2n$条棱。
对于60条棱的棱锥,设其为n棱锥,则有$2n=60$,解得$n=30$,即三十棱锥。
对于30条棱的棱柱,棱柱的棱数是其底面边数的3倍,设其为n棱柱,则有$3n=30$,解得$n=10$,即十棱柱。
四棱锥:底面是四边形,有4条边,加上4条侧棱,共有$4+4=8$条棱。
五棱锥:底面是五边形,有5条边,加上5条侧棱,共有$5+5=10$条棱。
n棱锥:底面是n边形,有n条边,加上n条侧棱,共有$n+n=2n$条棱。
对于60条棱的棱锥,设其为n棱锥,则有$2n=60$,解得$n=30$,即三十棱锥。
对于30条棱的棱柱,棱柱的棱数是其底面边数的3倍,设其为n棱柱,则有$3n=30$,解得$n=10$,即十棱柱。
(1)补全表格:
顶点数(V)、面数(F)、棱数(E)之间满足的关系式是
(2)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成的,且有24个顶点,每个顶点处都有3条棱. 设该多面体外表面的三角形的个数为x,八边形的个数为y,求x+y的值.
解:由题,该几何体共有24×3÷2=36(条)棱
24+x+y-36=2,解得x+y=14
6
12
6
顶点数(V)、面数(F)、棱数(E)之间满足的关系式是
V+F-E=2
.(2)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成的,且有24个顶点,每个顶点处都有3条棱. 设该多面体外表面的三角形的个数为x,八边形的个数为y,求x+y的值.
解:由题,该几何体共有24×3÷2=36(条)棱
24+x+y-36=2,解得x+y=14
答案:6
12
6
V+F-E=2
解:由题,该几何体共有24×3÷2=36(条)棱
24+x+y-36=2,解得x+y=14
12
6
V+F-E=2
解:由题,该几何体共有24×3÷2=36(条)棱
24+x+y-36=2,解得x+y=14