2. 如图,将一圆形纸片对折后再对折,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是 (
C
)答案:C
解析:
圆形纸片对折两次后形成直角扇形(四分之一圆),沿虚线剪开后,展开过程中图形关于两条互相垂直的折痕(直径)对称,最终形成四边相等的菱形。
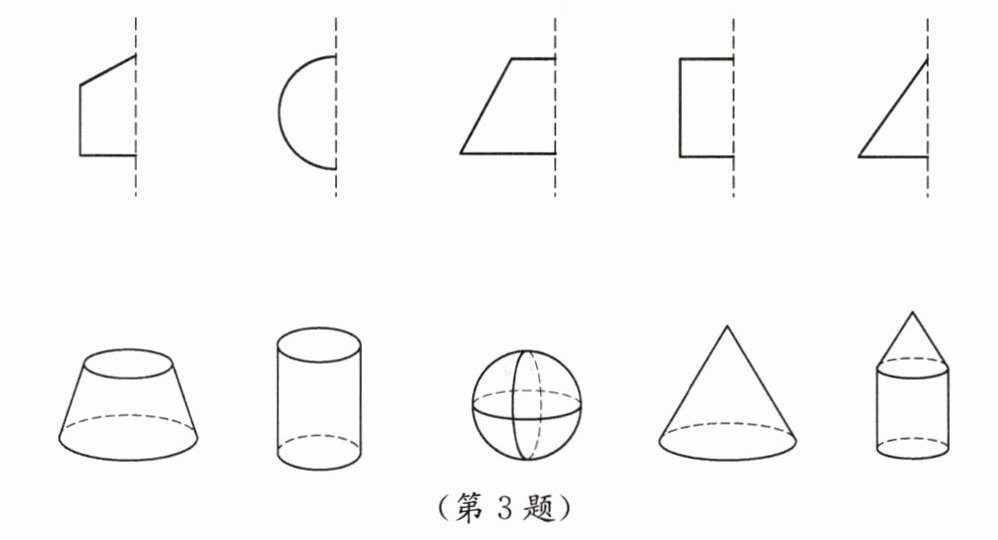
3. 如图,第一行的图形绕虚线旋转一周,便能形成第二行的某个几何体,用线连一连.

答案:
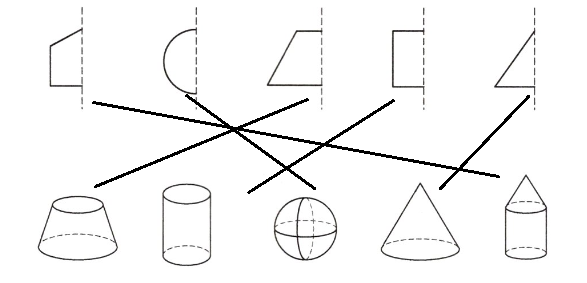

解析:
第一行第一个图形是直角梯形,绕虚线旋转一周后形成的是圆台。
第一行第二个图形是半圆,绕虚线旋转一周后形成的是球体。
第一行第三个图形是直角三角形,绕虚线旋转一周后形成的是圆锥。
第一行第四个图形是矩形,绕虚线旋转一周后形成的是圆柱。
第一行第二个图形是半圆,绕虚线旋转一周后形成的是球体。
第一行第三个图形是直角三角形,绕虚线旋转一周后形成的是圆锥。
第一行第四个图形是矩形,绕虚线旋转一周后形成的是圆柱。
1. 如图,在方格纸中,三角形 ABC 经过运动变化得到了三角形 DEF,正确的运动变化是 (
A.将三角形 ABC 绕点 C 按逆时针方向旋转 90°,再向下平移 2 格
B.将三角形 ABC 绕点 C 按顺时针方向旋转 90°,再向下平移 5 格
C.将三角形 ABC 向下平移 4 格,再绕点 C 按逆时针方向旋转 180°
D.将三角形 ABC 向下平移 5 格,再绕点 C 按顺时针方向旋转 180°
B
)A.将三角形 ABC 绕点 C 按逆时针方向旋转 90°,再向下平移 2 格
B.将三角形 ABC 绕点 C 按顺时针方向旋转 90°,再向下平移 5 格
C.将三角形 ABC 向下平移 4 格,再绕点 C 按逆时针方向旋转 180°
D.将三角形 ABC 向下平移 5 格,再绕点 C 按顺时针方向旋转 180°
答案:B
2. 用边长为 4 的正方形纸片剪出一副七巧板,并将其拼成如图的"小天鹅",则阴影部分的面积是 (
A.6
B.7
C.8
D.9
B
)A.6
B.7
C.8
D.9
答案:B
解析:
正方形面积为$4×4 = 16$。七巧板中,最小的等腰直角三角形面积为$\frac{1}{2}×(\sqrt{2})^2=1$,小正方形面积为$2$,平行四边形面积为$2$,中等等腰直角三角形面积为$2$,大等腰直角三角形面积为$4$。阴影部分由两个大等腰直角三角形组成,面积为$4 + 4=8$。
C
C
3. 按要求画图.

(1) 画出将三角形 ABC 向右平移 6 格,再向上平移 3 格后的三角形$ A_1B_1C_1;$
(2) 画出将三角形 ABC 绕点 B 按顺时针方向旋转 90°后的三角形$ A_2B_2C_2;$
(3) 画出将三角形 ABC 沿直线 EF 翻折后的三角形$ A_3B_3C.$

(1) 画出将三角形 ABC 向右平移 6 格,再向上平移 3 格后的三角形$ A_1B_1C_1;$
(2) 画出将三角形 ABC 绕点 B 按顺时针方向旋转 90°后的三角形$ A_2B_2C_2;$
(3) 画出将三角形 ABC 沿直线 EF 翻折后的三角形$ A_3B_3C.$
答案: