1. 下列各图形不能折叠成一个正方体的是 (
D
)答案:D
解析:
选项A、B、D经过折叠均能围成正方体,而选项C中折叠后有两个面重合,缺少一个侧面,所以不能折成正方体。
2. 直角三角形绕它斜边(即最长的边)旋转一周得到的几何体为 (
D
)答案:D
解析:
直角三角形绕它斜边旋转一周得到的几何体是由两个共底面的圆锥组合而成,只有选项D符合。
3. 一个几何体展开后的平面图形由四个等边三角形构成(如图),则原来的几何体是 (
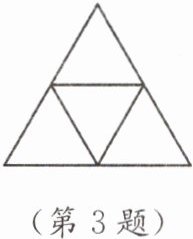
A.六面体
B.四棱锥
C.三棱锥
D.三棱柱
C
) 
A.六面体
B.四棱锥
C.三棱锥
D.三棱柱
答案:C
解析:
四张等边三角形纸片拼合在一起,底边相互重合,围成一个三棱锥的表面,因此该几何体为三棱锥。
4. 用一个平面去截一个正方体,若所得的截面是一个三角形,则留下的较大的一块几何体一定有 (
A.7 个面
B.15 条棱
C.7 个顶点
D.10 个顶点
A
)A.7 个面
B.15 条棱
C.7 个顶点
D.10 个顶点
答案:A
解析:
当用一个平面去截正方体得到三角形截面时,平面会与正方体的3个面相交,原正方体有6个面,截面为新增加的1个面,所以留下的较大几何体的面数为$6 - 3 + 1=4$个面?不对,应该是原正方体6个面,截去一部分后,截面成为新的面,所以面数是$6 + 1=7$个面。
对于棱数,原正方体12条棱,截面是三角形,会增加3条棱,同时截去部分会使原正方体的3条棱被截断,所以棱数为$12 - 3 + 3=12$条棱,不是15条。
顶点数,原正方体8个顶点,截去一个三棱锥,截去3个顶点,同时截面三角形有3个新顶点,所以顶点数为$8 - 3 + 3=8$个顶点,不是7个或10个。
综上,留下的较大的一块几何体一定有7个面。
A
对于棱数,原正方体12条棱,截面是三角形,会增加3条棱,同时截去部分会使原正方体的3条棱被截断,所以棱数为$12 - 3 + 3=12$条棱,不是15条。
顶点数,原正方体8个顶点,截去一个三棱锥,截去3个顶点,同时截面三角形有3个新顶点,所以顶点数为$8 - 3 + 3=8$个顶点,不是7个或10个。
综上,留下的较大的一块几何体一定有7个面。
A
5. 如图所示是一个正方体纸盒的平面展开图,请把数 8,-3,-15 分别填入余下的三个正方形中,使得将平面图形按虚线折成正方体后,相对面上的两个数互为相反数.


答案:8
-3
-15
-3
-15
解析:
1. 确定已知数的相反数:3的相反数是-3,15的相反数是-15,-8的相反数是8。
2. 判断正方体展开图中相对面:中间一行四个正方形中,第1个与第3个相对,第2个与第4个相对;上下两个正方形相对。
3. 对应填入相反数:-8的相对面(上面正方形)填8;3的相对面(中间一行第3个正方形)填-3;15的相对面(中间一行第4个正方形)填-15。
2. 判断正方体展开图中相对面:中间一行四个正方形中,第1个与第3个相对,第2个与第4个相对;上下两个正方形相对。
3. 对应填入相反数:-8的相对面(上面正方形)填8;3的相对面(中间一行第3个正方形)填-3;15的相对面(中间一行第4个正方形)填-15。
某种产品的包装盒是长方体,已知其长为 8 cm,展开图及尺寸如图所示.
(1)求长方体包装盒的体积;
(2)请设计一种外包装纸箱,使每箱能装 10 件这种包装盒,要求没有空隙且要使该外包装纸箱所用的材料尽可能少(即纸箱的表面积尽可能小).

(1)求长方体包装盒的体积;
(2)请设计一种外包装纸箱,使每箱能装 10 件这种包装盒,要求没有空隙且要使该外包装纸箱所用的材料尽可能少(即纸箱的表面积尽可能小).

答案:解$:$
$(1)$由图可得$,$高$+$宽$+$高$=12cm,$设高为$xcm,$则宽为$(12-2x)cm$
宽$+$长$+$高$+$长$=25cm,$即$12-2x+8+x+8=25,$解得$x=3$
$12-2x=6$
∴高为$3cm,$宽为$6cm$
∴体积为$3×6×8=144(cm^{3})$
$(2)$底面面积$6×8=48(cm^{2}) $侧面面积分别为$3×6=18(cm^{2}),3×8=24(cm^{2})$
要使材料尽可能少$,$则要尽可能用底面重叠
这样可用$15×6×8$的包装纸箱$,$再考虑$15×8$面积最大$,$则设计$15×12×8$规格
则表面积为$(8×12+8×15+12×15)×2=792(cm^{2})$
∴规格为$15×12×8cm$
$(1)$由图可得$,$高$+$宽$+$高$=12cm,$设高为$xcm,$则宽为$(12-2x)cm$
宽$+$长$+$高$+$长$=25cm,$即$12-2x+8+x+8=25,$解得$x=3$
$12-2x=6$
∴高为$3cm,$宽为$6cm$
∴体积为$3×6×8=144(cm^{3})$
$(2)$底面面积$6×8=48(cm^{2}) $侧面面积分别为$3×6=18(cm^{2}),3×8=24(cm^{2})$
要使材料尽可能少$,$则要尽可能用底面重叠
这样可用$15×6×8$的包装纸箱$,$再考虑$15×8$面积最大$,$则设计$15×12×8$规格
则表面积为$(8×12+8×15+12×15)×2=792(cm^{2})$
∴规格为$15×12×8cm$
解析:
(1)设长方体包装盒的宽为$b\ cm$,高为$h\ cm$,已知长$a = 8\ cm$。
由展开图尺寸关系得:
$\begin{cases}2a + h = 25\\b + h = 12\end{cases}$
将$a = 8$代入$2a + h = 25$,得$2×8 + h = 25$,解得$h = 9$。
将$h = 9$代入$b + h = 12$,得$b = 12 - 9 = 3$。
体积$V = a× b× h = 8×3×9 = 216\ cm^3$。
(2)10件包装盒的总体积为$10×216 = 2160\ cm^3$。要使外包装纸箱表面积最小,需使长宽高尽可能接近。
10分解为$2×5×1$,小长方体尺寸$8\ cm,3\ cm,9\ cm$,组合得大长方体尺寸:
$8×2 = 16\ cm$,$3×5 = 15\ cm$,$9×1 = 9\ cm$。
表面积$S = 2(16×15 + 16×9 + 15×9) = 2(240 + 144 + 135) = 1038\ cm^2$。