2. 如图,甲、乙两人沿同一直线同时出发去往 B 地,甲到达 B 地后立即以原速沿原路返回,乙到达 B 地后停止运动,已知运动过程中两人到 B 地的距离 y km 与出发时间 t h 的关系如图所示,则甲、乙两人在出发后

20/3
h 第一次相遇.
答案:20/3
解析:
由图可知,甲从出发地到B地再返回,总路程160km(往返各80km),总时间10h,故甲的速度为160÷10=16km/h,单程时间为80÷16=5h,即甲5h到达B地(a=5)。
甲去程:y甲1=-16t+80(0≤t≤5);甲回程:y甲2=16t-80(5<t≤10)。
乙从出发地到B地,设乙的速度为v,其到B地距离y乙=80-vt。由图可知乙10h到达B地,故v=80÷10=8km/h,即y乙=-8t+80(0≤t≤10)。
甲乙第一次相遇在甲回程时,联立y甲2与y乙:16t-80=-8t+80,解得t=20/3。
甲去程:y甲1=-16t+80(0≤t≤5);甲回程:y甲2=16t-80(5<t≤10)。
乙从出发地到B地,设乙的速度为v,其到B地距离y乙=80-vt。由图可知乙10h到达B地,故v=80÷10=8km/h,即y乙=-8t+80(0≤t≤10)。
甲乙第一次相遇在甲回程时,联立y甲2与y乙:16t-80=-8t+80,解得t=20/3。
3. “每天一杯纯牛奶”是一种便捷的营养补充方式,有助于身体健康.某乳品公司每月均需通过快递公司向 A 地输送一批牛奶.快递公司给出三种运费方案,具体如下:
方案一:每千克运费 0.45 元,按实际运输质量结算;
方案二:每月收取 600 元管理费用,再每千克运费 0.15 元;
方案三:每月收取 1350 元包干,不限运输质量.
设该公司每月运输牛奶 x kg.选择方案一时,运费为$ y_1$元;选择方案二时,运费为$ y_2$元;选择方案三时,运费为$ y_3$元.
(1)请直接写出$ y_1,y_2,y_3$关于 x 的表达式;
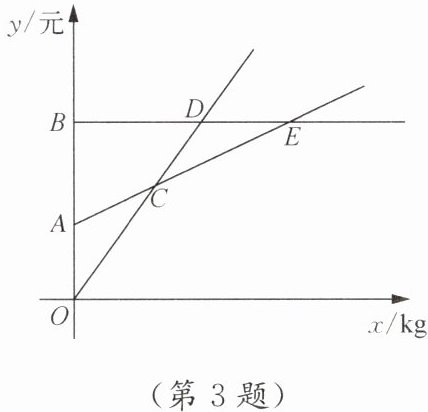
(2)在同一平面直角坐标系中,三种方案对应的函数图象如图所示,求出点 C,D,E 的坐标,并直接写出如何选择方案更合算.
方案一:每千克运费 0.45 元,按实际运输质量结算;
方案二:每月收取 600 元管理费用,再每千克运费 0.15 元;
方案三:每月收取 1350 元包干,不限运输质量.
设该公司每月运输牛奶 x kg.选择方案一时,运费为$ y_1$元;选择方案二时,运费为$ y_2$元;选择方案三时,运费为$ y_3$元.
(1)请直接写出$ y_1,y_2,y_3$关于 x 的表达式;
(2)在同一平面直角坐标系中,三种方案对应的函数图象如图所示,求出点 C,D,E 的坐标,并直接写出如何选择方案更合算.

答案:(1)
$y_1 = 0.45x$;
$y_2=0.15x + 600$;
$y_3 = 1350$。
(2)
求点$C$坐标:
令$y_1=y_2$,即$0.45x=0.15x + 600$,
$0.45x-0.15x=600$,
$0.3x=600$,
解得$x = 2000$,
把$x = 2000$代入$y_1=0.45×2000 = 900$,
所以$C(2000,900)$。
求点$D$坐标:
令$y_2=y_3$,即$0.15x + 600=1350$,
$0.15x=1350 - 600$,
$0.15x=750$,
解得$x = 5000$,
所以$D(5000,1350)$。
求点$E$坐标:
令$y_1=y_3$,即$0.45x=1350$,
解得$x = 3000$,
所以$E(3000,1350)$。
方案选择:
当$0\lt x\lt2000$时,$y_1\lt y_2$,$y_1\lt y_3$,选择方案一更合算;
当$x = 2000$时,$y_1=y_2\lt y_3$,选择方案一或方案二一样合算;
当$2000\lt x\lt5000$时,$y_2\lt y_1$,$y_2\lt y_3$,选择方案二更合算;
当$x = 5000$时,$y_2=y_3\lt y_1$,选择方案二或方案三一样合算;
当$x\gt5000$时,$y_3\lt y_2$,$y_3\lt y_1$,选择方案三更合算。
$y_1 = 0.45x$;
$y_2=0.15x + 600$;
$y_3 = 1350$。
(2)
求点$C$坐标:
令$y_1=y_2$,即$0.45x=0.15x + 600$,
$0.45x-0.15x=600$,
$0.3x=600$,
解得$x = 2000$,
把$x = 2000$代入$y_1=0.45×2000 = 900$,
所以$C(2000,900)$。
求点$D$坐标:
令$y_2=y_3$,即$0.15x + 600=1350$,
$0.15x=1350 - 600$,
$0.15x=750$,
解得$x = 5000$,
所以$D(5000,1350)$。
求点$E$坐标:
令$y_1=y_3$,即$0.45x=1350$,
解得$x = 3000$,
所以$E(3000,1350)$。
方案选择:
当$0\lt x\lt2000$时,$y_1\lt y_2$,$y_1\lt y_3$,选择方案一更合算;
当$x = 2000$时,$y_1=y_2\lt y_3$,选择方案一或方案二一样合算;
当$2000\lt x\lt5000$时,$y_2\lt y_1$,$y_2\lt y_3$,选择方案二更合算;
当$x = 5000$时,$y_2=y_3\lt y_1$,选择方案二或方案三一样合算;
当$x\gt5000$时,$y_3\lt y_2$,$y_3\lt y_1$,选择方案三更合算。