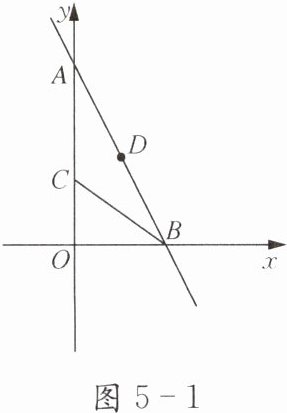
1. 如图5-1,在平面直角坐标系中,一次函数$y= -2x+8$的图象与y轴交于点A,与x轴交于点B;在y轴上取一点C,$AC= BC$,连接BC.
(1)求点C的坐标和直线BC相应的函数表达式;
(2)在线段AB上取一点D,若点D的横坐标为2,请在x轴上找一点P,使得$PD+PC$的值最小,并求出此时点P的坐标.
(1)求点C的坐标和直线BC相应的函数表达式;
(2)在线段AB上取一点D,若点D的横坐标为2,请在x轴上找一点P,使得$PD+PC$的值最小,并求出此时点P的坐标.

答案:(1)对于一次函数$y=-2x+8$,
令$x=0$,得$y=8$,则$A(0,8)$;令$y=0$,得$-2x+8=0$,$x=4$,则$B(4,0)$。
设$C(0,c)$,$AC=|8-c|$,$BC=\sqrt{(4-0)^2+(0-c)^2}=\sqrt{16+c^2}$。
由$AC=BC$,得$|8-c|=\sqrt{16+c^2}$,两边平方:$(8-c)^2=16+c^2$,
即$64-16c+c^2=16+c^2$,解得$c=3$,故$C(0,3)$。
设直线$BC$:$y=kx+b$,将$B(4,0)$,$C(0,3)$代入,得$\begin{cases}4k+b=0\\b=3\end{cases}$,
解得$k=-\frac{3}{4}$,$b=3$,故直线$BC$:$y=-\frac{3}{4}x+3$。
(2)在$y=-2x+8$中,令$x=2$,得$y=4$,则$D(2,4)$。
作$C(0,3)$关于$x$轴的对称点$C'(0,-3)$,连接$DC'$交$x$轴于$P$,此时$PD+PC$最小。
设直线$DC'$:$y=mx+n$,将$D(2,4)$,$C'(0,-3)$代入,得$\begin{cases}2m+n=4\\n=-3\end{cases}$,
解得$m=\frac{7}{2}$,$n=-3$,故直线$DC'$:$y=\frac{7}{2}x-3$。
令$y=0$,得$\frac{7}{2}x-3=0$,$x=\frac{6}{7}$,则$P\left(\frac{6}{7},0\right)$。
(1)$C(0,3)$,直线$BC$:$y=-\frac{3}{4}x+3$;(2)$P\left(\frac{6}{7},0\right)$。
令$x=0$,得$y=8$,则$A(0,8)$;令$y=0$,得$-2x+8=0$,$x=4$,则$B(4,0)$。
设$C(0,c)$,$AC=|8-c|$,$BC=\sqrt{(4-0)^2+(0-c)^2}=\sqrt{16+c^2}$。
由$AC=BC$,得$|8-c|=\sqrt{16+c^2}$,两边平方:$(8-c)^2=16+c^2$,
即$64-16c+c^2=16+c^2$,解得$c=3$,故$C(0,3)$。
设直线$BC$:$y=kx+b$,将$B(4,0)$,$C(0,3)$代入,得$\begin{cases}4k+b=0\\b=3\end{cases}$,
解得$k=-\frac{3}{4}$,$b=3$,故直线$BC$:$y=-\frac{3}{4}x+3$。
(2)在$y=-2x+8$中,令$x=2$,得$y=4$,则$D(2,4)$。
作$C(0,3)$关于$x$轴的对称点$C'(0,-3)$,连接$DC'$交$x$轴于$P$,此时$PD+PC$最小。
设直线$DC'$:$y=mx+n$,将$D(2,4)$,$C'(0,-3)$代入,得$\begin{cases}2m+n=4\\n=-3\end{cases}$,
解得$m=\frac{7}{2}$,$n=-3$,故直线$DC'$:$y=\frac{7}{2}x-3$。
令$y=0$,得$\frac{7}{2}x-3=0$,$x=\frac{6}{7}$,则$P\left(\frac{6}{7},0\right)$。
(1)$C(0,3)$,直线$BC$:$y=-\frac{3}{4}x+3$;(2)$P\left(\frac{6}{7},0\right)$。