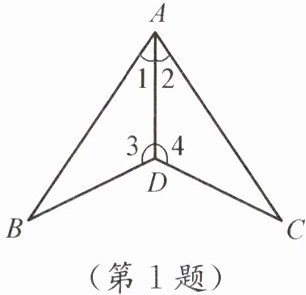
1. 如图,∠1= ∠2,∠3= ∠4,要证明BD= CD,证明中判定两个三角形全等的依据是(
A.角角角
B.角边角
C.边角边
D.角角边
D
)
A.角角角
B.角边角
C.边角边
D.角角边
答案:D
2. 如图,在△ABC和△DEF中,AB= DE,∠B= ∠DEF. 下列选项中,添加为已知条件后仍无法使△ABC≌△DEF的是(

A.BC= EF
B.∠A= ∠D
C.AC= DF
D.BE= CF
C
)
A.BC= EF
B.∠A= ∠D
C.AC= DF
D.BE= CF
答案:C
解析:
选项A,由于$AB=DE,\angle B=\angle DEF,BC=EF$,根据$SAS$判定定理,可以得出$\triangle ABC\cong\triangle DEF$,所以选项A不符合题意;
选项B,由于$AB=DE,\angle B=\angle DEF,\angle A=\angle D$,根据$ASA$判定定理,可以得出$\triangle ABC\cong\triangle DEF$,所以选项B不符合题意;
选项C,由于$AB=DE,\angle B=\angle DEF,AC=DF$,是$SSA$,无法判定$\triangle ABC\cong\triangle DEF$,所以选项C符合题意;
选项D,由于$BE=CF$,所以$BE+EC=CF+EC$,即$BC=EF$,又$AB=DE,\angle B=\angle DEF$,根据$SAS$判定定理,可以得出$\triangle ABC\cong\triangle DEF$,所以选项D不符合题意。
选项B,由于$AB=DE,\angle B=\angle DEF,\angle A=\angle D$,根据$ASA$判定定理,可以得出$\triangle ABC\cong\triangle DEF$,所以选项B不符合题意;
选项C,由于$AB=DE,\angle B=\angle DEF,AC=DF$,是$SSA$,无法判定$\triangle ABC\cong\triangle DEF$,所以选项C符合题意;
选项D,由于$BE=CF$,所以$BE+EC=CF+EC$,即$BC=EF$,又$AB=DE,\angle B=\angle DEF$,根据$SAS$判定定理,可以得出$\triangle ABC\cong\triangle DEF$,所以选项D不符合题意。
3. 如图,AE= AD,要使△ABD≌△ACE,需要添加的一个条件是

AB=AC(答案不唯一)
.
答案:AB=AC(答案不唯一)。
解析:
根据题意,已知AE=AD,要使△ABD≌△ACE,可以使用“边-角-边”(SAS)全等判定法。
在△ABD和△ACE中,
添加条件∠A=∠A,AB=AC后,
在△ABD和△ACE中,
$\left\{\begin{matrix}AD=AE,\\\angle A=\angle A,\\AB=AC.\end{matrix}\right.$
根据SAS全等判定法,可以判定△ABD≌△ACE。
所以需要添加的条件可以是AB=AC(答案不唯一)。
也可以添加∠B=∠C,此时运用的是AAS的全等判定方法。
还可以添加∠ADB=∠AEC,此时运用的是ASA的全等判定方法。
在△ABD和△ACE中,
添加条件∠A=∠A,AB=AC后,
在△ABD和△ACE中,
$\left\{\begin{matrix}AD=AE,\\\angle A=\angle A,\\AB=AC.\end{matrix}\right.$
根据SAS全等判定法,可以判定△ABD≌△ACE。
所以需要添加的条件可以是AB=AC(答案不唯一)。
也可以添加∠B=∠C,此时运用的是AAS的全等判定方法。
还可以添加∠ADB=∠AEC,此时运用的是ASA的全等判定方法。
4. 已知:如图,∠1= ∠2,∠3= ∠4,点E在BD上,连接AE,CE.
求证:AE= CE.

求证:AE= CE.

答案:证明:
在△ABD和△CBD中,
∵∠1=∠2(已知),
BD=BD(公共边),
∠3=∠4(已知),
∴△ABD≌△CBD(ASA)。
∴AB=CB(全等三角形对应边相等)。
在△ABE和△CBE中,
AB=CB(已证),
∠1=∠2(已知),
BE=BE(公共边),
∴△ABE≌△CBE(SAS)。
∴AE=CE(全等三角形对应边相等)。
在△ABD和△CBD中,
∵∠1=∠2(已知),
BD=BD(公共边),
∠3=∠4(已知),
∴△ABD≌△CBD(ASA)。
∴AB=CB(全等三角形对应边相等)。
在△ABE和△CBE中,
AB=CB(已证),
∠1=∠2(已知),
BE=BE(公共边),
∴△ABE≌△CBE(SAS)。
∴AE=CE(全等三角形对应边相等)。
1. 如图,一块三角形的玻璃被打碎成3块,现要到玻璃店去配一块完全一样的玻璃,只要(

A.带碎片①去
B.带碎片②去
C.带碎片③去
D.带碎片①和②去
C
)
A.带碎片①去
B.带碎片②去
C.带碎片③去
D.带碎片①和②去
答案:C
解析:
碎片③保留了原三角形的两个角和它们的夹边,根据“角边角”(ASA)判定定理,可配出完全一样的玻璃。碎片①只有一个角,碎片②仅保留部分边和角,均无法确定原三角形形状。
2. 如图,在△ABC中,BE//CF,BE,CF与AE的交点分别为E,F.
(1) 若AD是△ABC的中线,则BE与CF相等吗?
(2) 若BE= CF,则AD是△ABC的中线吗?为什么?

(1) 若AD是△ABC的中线,则BE与CF相等吗?
(2) 若BE= CF,则AD是△ABC的中线吗?为什么?

答案:(1)$BE=CF$。
证明:
$\because BE// CF$,
$\therefore \angle FCD=\angle EBD$,$\angle CFD=\angle BED$,
$\because AD$是$\triangle ABC$的中线,
$\therefore BD=CD$。
在$\triangle BDE$和$\triangle CDF$中,
$\begin{cases}\angle FCD=\angle EBD,\\\angle CFD=\angle BED,\\BD=CD.\end{cases}$
$\therefore \triangle BDE\cong \triangle CDF(AAS)$,
$\therefore BE=CF$。
(2)$AD$是$\triangle ABC$的中线。
证明:
$\because BE// CF$,
$\therefore \angle FCD=\angle EBD$,$\angle CFD=\angle BED$,
在$\triangle BDE$和$\triangle CDF$中,
$\begin{cases}\angle FCD=\angle EBD,\\\angle CFD=\angle BED,\\BE=CF.\end{cases}$
$\therefore \triangle BDE\cong \triangle CDF(AAS)$,
$\therefore BD=CD$,
$\therefore AD$是$\triangle ABC$的中线。
证明:
$\because BE// CF$,
$\therefore \angle FCD=\angle EBD$,$\angle CFD=\angle BED$,
$\because AD$是$\triangle ABC$的中线,
$\therefore BD=CD$。
在$\triangle BDE$和$\triangle CDF$中,
$\begin{cases}\angle FCD=\angle EBD,\\\angle CFD=\angle BED,\\BD=CD.\end{cases}$
$\therefore \triangle BDE\cong \triangle CDF(AAS)$,
$\therefore BE=CF$。
(2)$AD$是$\triangle ABC$的中线。
证明:
$\because BE// CF$,
$\therefore \angle FCD=\angle EBD$,$\angle CFD=\angle BED$,
在$\triangle BDE$和$\triangle CDF$中,
$\begin{cases}\angle FCD=\angle EBD,\\\angle CFD=\angle BED,\\BE=CF.\end{cases}$
$\therefore \triangle BDE\cong \triangle CDF(AAS)$,
$\therefore BD=CD$,
$\therefore AD$是$\triangle ABC$的中线。