1. 关于函数$y= -2x+1$,下列结论中,正确的是(
A.图象必经过点$(-2,1)$
B.图象经过第一、二、三象限
C.图象与一次函数$y= -2x+3$的图象平行
D.y随x的增大而增大
C
)A.图象必经过点$(-2,1)$
B.图象经过第一、二、三象限
C.图象与一次函数$y= -2x+3$的图象平行
D.y随x的增大而增大
答案:C
解析:
A. 对于函数$y = -2x + 1$,当$x = -2$时,$y = -2×(-2) + 1 = 5$,所以图象不经过点$(-2,1)$,故A选项错误;
B. 函数$y = -2x + 1$的斜率为$-2$,小于0,截距为$1$,大于0,所以图象经过第一、二、四象限,不经过第三象限,故B选项错误;
C. 函数$y = -2x + 1$与$y = -2x + 3$的斜率都是$-2$,所以它们的图象平行,故C选项正确;
D. 函数$y = -2x + 1$的斜率为$-2$,小于0,所以$y$随$x$的增大而减小,故D选项错误。
B. 函数$y = -2x + 1$的斜率为$-2$,小于0,截距为$1$,大于0,所以图象经过第一、二、四象限,不经过第三象限,故B选项错误;
C. 函数$y = -2x + 1$与$y = -2x + 3$的斜率都是$-2$,所以它们的图象平行,故C选项正确;
D. 函数$y = -2x + 1$的斜率为$-2$,小于0,所以$y$随$x$的增大而减小,故D选项错误。
2. 若一次函数$y= kx+b(k,b是常数,k≠0)的图象过点A(3,2)$,则关于x的方程$kx+2k+b= 2$的解为
1
.答案:1(或 $x = 1$,根据题目要求选择合适的答案格式)
解析:
1. 已知一次函数 $y = kx + b$ 的图象过点 $A(3,2)$,根据一次函数的定义,当 $x = 3$ 时,$y = 2$。
2. 代入点 $A(3,2)$ 到函数 $y = kx + b$ 中,得到 $3k + b = 2$。
3. 考虑方程 $kx + 2k + b = 2$,将其改写为 $k(x + 2) + b = 2$。
4. 由于 $3k + b = 2$,我们可以发现当 $x + 2 = 3$ 时,即 $x = 1$,方程 $k(x + 2) + b = 2$ 成立。
5. 因此,方程 $kx + 2k + b = 2$ 的解为 $x = 1$。
2. 代入点 $A(3,2)$ 到函数 $y = kx + b$ 中,得到 $3k + b = 2$。
3. 考虑方程 $kx + 2k + b = 2$,将其改写为 $k(x + 2) + b = 2$。
4. 由于 $3k + b = 2$,我们可以发现当 $x + 2 = 3$ 时,即 $x = 1$,方程 $k(x + 2) + b = 2$ 成立。
5. 因此,方程 $kx + 2k + b = 2$ 的解为 $x = 1$。
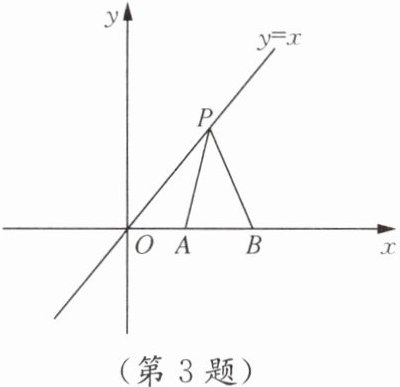
3. 在如图所示的平面直角坐标系中,点P是一次函数$y= x$图象上的动点,$A(1,0),B(2,0)$是x轴上的两点,则$PA+PB$的最小值为
$\sqrt{5}$
.
答案:$\sqrt{5}$
解析:
作点$A$关于直线$y = x$的对称点$A'$。
由于$A(1,0)$,根据关于直线$y = x$对称的点的坐标特征,可得$A'(0,1)$。
连接$A'B$,与直线$y = x$的交点即为使$PA + PB$最小的点$P$。
此时$PA + PB = PA' + PB = A'B$(根据两点之间线段最短)。
已知$B(2,0)$,$A'(0,1)$,根据两点间距离公式$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$,可得:
$A'B=\sqrt{(2 - 0)^2 + (0 - 1)^2}=\sqrt{4 + 1}=\sqrt{5}$。
所以$PA + PB$的最小值为$\sqrt{5}$。
由于$A(1,0)$,根据关于直线$y = x$对称的点的坐标特征,可得$A'(0,1)$。
连接$A'B$,与直线$y = x$的交点即为使$PA + PB$最小的点$P$。
此时$PA + PB = PA' + PB = A'B$(根据两点之间线段最短)。
已知$B(2,0)$,$A'(0,1)$,根据两点间距离公式$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$,可得:
$A'B=\sqrt{(2 - 0)^2 + (0 - 1)^2}=\sqrt{4 + 1}=\sqrt{5}$。
所以$PA + PB$的最小值为$\sqrt{5}$。
4. 如图,已知函数$y= x+1$的图象与y轴交于点A,一次函数$y= kx+b的图象经过点B(0,-1)$,与x轴以及$y= x+1$的图象分别交于点C,D,且点D的坐标为$(1,n)$.
(1)求一次函数$y= kx+b$的表达式.
(2)求四边形AOCD的面积.
(3)在平面内直线CD的右侧是否存在点P,使得以点P,C,D为顶点的三角形是以CD为腰的等腰直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

(1)求一次函数$y= kx+b$的表达式.
(2)求四边形AOCD的面积.
(3)在平面内直线CD的右侧是否存在点P,使得以点P,C,D为顶点的三角形是以CD为腰的等腰直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

答案:(1) 因为点D(1,n)在y=x+1上,所以n=1+1=2,即D(1,2)。又一次函数y=kx+b过点B(0,-1)和D(1,2),将B(0,-1)代入得b=-1,将D(1,2)代入y=kx-1得2=k-1,解得k=3,故表达式为y=3x-1。
(2) A为y=x+1与y轴交点,A(0,1);C为y=3x-1与x轴交点,令y=0得x=1/3,即C(1/3,0);O(0,0),D(1,2)。四边形AOCD面积=S△AOD+S△OCD。S△AOD=1/2×OA×1=1/2×1×1=1/2;S△OCD=1/2×OC×2=1/2×(1/3)×2=1/3。总面积=1/2+1/3=5/6。
(3) 存在,点P坐标为(7/3,-2/3)和(3,4/3)。
(2) A为y=x+1与y轴交点,A(0,1);C为y=3x-1与x轴交点,令y=0得x=1/3,即C(1/3,0);O(0,0),D(1,2)。四边形AOCD面积=S△AOD+S△OCD。S△AOD=1/2×OA×1=1/2×1×1=1/2;S△OCD=1/2×OC×2=1/2×(1/3)×2=1/3。总面积=1/2+1/3=5/6。
(3) 存在,点P坐标为(7/3,-2/3)和(3,4/3)。