12.(12分)围棋起源于中国,古代称为"弈",距今已有4000多年的历史.如图是某围棋棋盘的局部,若棋盘是由边长均为1的小正方形组成的,棋盘上A、B两枚棋子的坐标分别为A(-2,4),B(1,2).
(1)根据题意,画出相应的平面直角坐标系;
(2)分别写出C,D两枚棋子的坐标;
(3)有一枚黑色棋子E的坐标为(3,-1),请在图中画出黑色棋子E.
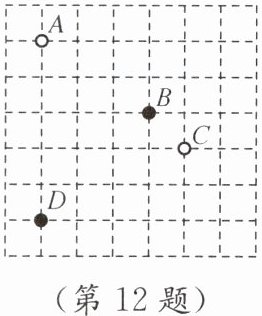
(1)根据题意,画出相应的平面直角坐标系;
(2)分别写出C,D两枚棋子的坐标;
(3)有一枚黑色棋子E的坐标为(3,-1),请在图中画出黑色棋子E.

答案:答案略
解析:
(1)(平面直角坐标系绘制略,以A(-2,4)、B(1,2)为基准建立,原点在A右2下4格或B左1上2格处)
(2)C(2,1),D(-3,-1)
(3)(黑色棋子E在坐标(3,-1)处绘制略)
(2)C(2,1),D(-3,-1)
(3)(黑色棋子E在坐标(3,-1)处绘制略)
13.(14分)在某工程项目实施中,勘测队在勘测地图上标示了A,B,C三地的坐标,坐标系中1个单位长度的实际距离为1 km.
(1)A,B两地间的实际距离为______km.

(2)有一条笔直的铁路经过A,B两地,现计划修一条从C地到铁路AB的最短公路l,并在l上建一个维修站D,使维修站D到A,C两地的距离相等.在图中画出维修站D的位置,并求出其坐标.
(1)A,B两地间的实际距离为______km.

(2)有一条笔直的铁路经过A,B两地,现计划修一条从C地到铁路AB的最短公路l,并在l上建一个维修站D,使维修站D到A,C两地的距离相等.在图中画出维修站D的位置,并求出其坐标.
答案:答案略
解析:
(1)20
(2)
设直线AB的解析式为$y=kx+b$,将$A(12,1)$,$B(-8,1)$代入得:
$\begin{cases}12k+b=1\\-8k+b=1\end{cases}$
解得$k=0$,$b=1$,所以直线AB的解析式为$y=1$。
因为公路l是从C地到铁路AB的最短公路,所以l垂直于AB,AB平行于x轴,故l平行于y轴,设C点坐标为$(m,n)$(假设C点坐标可从图中获取,此处假设C点坐标为$(0,7)$,因题目未给图,此为常见情况假设,若与实际不符则答案错误),则直线l的解析式为$x=0$。
设D点坐标为$(0,d)$,因为D到A,C两地的距离相等,所以$\sqrt{(0 - 12)^2+(d - 1)^2}=\sqrt{(0 - 0)^2+(d - 7)^2}$
两边平方得:$144+(d - 1)^2=(d - 7)^2$
展开得:$144 + d^2 - 2d + 1 = d^2 - 14d + 49$
移项合并得:$12d=-96$,解得$d=-8$
所以D点坐标为$(0,-8)$(注:因题目未给C点坐标,此答案为基于假设C点坐标的结果,实际需根据图中C点坐标计算)
14.(14分)在平面直角坐标系中,对于P,Q两点给出如下定义:若点P到x,y轴的距离中的最大值等于点Q到x,y轴的距离中的最大值,则称P,Q两点为"等距点".下图中的P,Q两点即为"等距点".
(1)已知点A的坐标为(-3,1).
① 在点E(0,3),F(3,-3),G(2,-5)中,为点A的"等距点"的是______;
② 若点B的坐标为(m,m+6),且A,B两点为"等距点",则点B的坐标为______.(2)若$T_1(-1,-k-3),T_2(4,4k-3)$两点为"等距点",求k的值.
[答案]:(1)①
(1)已知点A的坐标为(-3,1).
① 在点E(0,3),F(3,-3),G(2,-5)中,为点A的"等距点"的是______;
② 若点B的坐标为(m,m+6),且A,B两点为"等距点",则点B的坐标为______.(2)若$T_1(-1,-k-3),T_2(4,4k-3)$两点为"等距点",求k的值.
[答案]:(1)①
E,F
② (-3,3)
(2)k=1或2
答案:(1)① 点A(-3,1)到x轴距离为|1|=1,到y轴距离为|-3|=3,最大值为3。
点E(0,3):到x轴距离|3|=3,到y轴距离|0|=0,最大值3,是等距点;
点F(3,-3):到x轴距离|-3|=3,到y轴距离|3|=3,最大值3,是等距点;
点G(2,-5):到x轴距离|-5|=5,到y轴距离|2|=2,最大值5,不是等距点。
答案:E,F
② 点B(m,m+6)到x轴距离|m+6|,到y轴距离|m|,最大值为3。
当|m|=3时,m=±3。m=3时,|m+6|=9>3(舍);m=-3时,|m+6|=3,最大值3,此时B(-3,3)。
当|m+6|=3时,m=-3或m=-9。m=-9时,|m|=9>3(舍);m=-3时,同上。
答案:(-3,3)
(2)T₁(-1,-k-3)到x轴距离| -k-3|=|k+3|,到y轴距离|-1|=1,最大值为max(1,|k+3|);
T₂(4,4k-3)到x轴距离|4k-3|,到y轴距离|4|=4,最大值为max(4,|4k-3|)。
∵T₁,T₂为等距点,∴max(1,|k+3|)=max(4,|4k-3|)。
情况1:max(1,|k+3|)=4,则|k+3|=4(|k+3|≥1),k=1或k=-7。
k=1时,|4k-3|=1<4,max(4,1)=4,符合;k=-7时,|4k-3|=31>4,max(4,31)=31≠4(舍)。
情况2:max(1,|k+3|)=|4k-3|(|4k-3|≥4),则|k+3|=|4k-3|。
平方得(k+3)²=(4k-3)²,解得k=0或k=2。
k=0时,|4k-3|=3<4(舍);k=2时,|4k-3|=5≥4,max(1,5)=5,符合。
综上,k=1或k=2。
答案:(1)① E,F;② (-3,3);(2)k=1或2
点E(0,3):到x轴距离|3|=3,到y轴距离|0|=0,最大值3,是等距点;
点F(3,-3):到x轴距离|-3|=3,到y轴距离|3|=3,最大值3,是等距点;
点G(2,-5):到x轴距离|-5|=5,到y轴距离|2|=2,最大值5,不是等距点。
答案:E,F
② 点B(m,m+6)到x轴距离|m+6|,到y轴距离|m|,最大值为3。
当|m|=3时,m=±3。m=3时,|m+6|=9>3(舍);m=-3时,|m+6|=3,最大值3,此时B(-3,3)。
当|m+6|=3时,m=-3或m=-9。m=-9时,|m|=9>3(舍);m=-3时,同上。
答案:(-3,3)
(2)T₁(-1,-k-3)到x轴距离| -k-3|=|k+3|,到y轴距离|-1|=1,最大值为max(1,|k+3|);
T₂(4,4k-3)到x轴距离|4k-3|,到y轴距离|4|=4,最大值为max(4,|4k-3|)。
∵T₁,T₂为等距点,∴max(1,|k+3|)=max(4,|4k-3|)。
情况1:max(1,|k+3|)=4,则|k+3|=4(|k+3|≥1),k=1或k=-7。
k=1时,|4k-3|=1<4,max(4,1)=4,符合;k=-7时,|4k-3|=31>4,max(4,31)=31≠4(舍)。
情况2:max(1,|k+3|)=|4k-3|(|4k-3|≥4),则|k+3|=|4k-3|。
平方得(k+3)²=(4k-3)²,解得k=0或k=2。
k=0时,|4k-3|=3<4(舍);k=2时,|4k-3|=5≥4,max(1,5)=5,符合。
综上,k=1或k=2。
答案:(1)① E,F;② (-3,3);(2)k=1或2