1. 9的算术平方根是(
A.3
B.$\sqrt{3}$
C.$\pm 3$
D.$\pm \sqrt{3}$
A
)A.3
B.$\sqrt{3}$
C.$\pm 3$
D.$\pm \sqrt{3}$
答案:A
解析:
根据算术平方根的定义,若一个非负数$x$的平方等于$a$,即$x^2 = a$,那么这个数$x$叫做$a$的算术平方根。因为$3^2 = 9$,所以$9$的算术平方根是$3$。
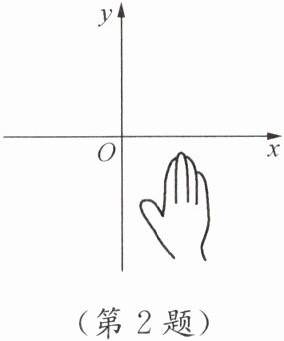
2. 如图,小手盖住的点的坐标可能为(
A.$(-4,-6)$
B.$(-6,3)$
C.$(3,-4)$
D.$(5,2)$
C
)
A.$(-4,-6)$
B.$(-6,3)$
C.$(3,-4)$
D.$(5,2)$
答案:C
解析:
从图中可以看出,小手盖住的点位于第四象限。
在平面直角坐标系中,第四象限的点具有正的横坐标和负的纵坐标。
选项A的坐标为$(-4, -6)$,横坐标为负,纵坐标为负,位于第三象限,不符合要求。
选项B的坐标为$(-6, 3)$,横坐标为负,纵坐标为正,位于第二象限,不符合要求。
选项C的坐标为$(3, -4)$,横坐标为正,纵坐标为负,位于第四象限,符合要求。
选项D的坐标为$(5, 2)$,横坐标为正,纵坐标为正,位于第一象限,不符合要求。
因此,小手盖住的点的坐标可能为$(3, -4)$。
在平面直角坐标系中,第四象限的点具有正的横坐标和负的纵坐标。
选项A的坐标为$(-4, -6)$,横坐标为负,纵坐标为负,位于第三象限,不符合要求。
选项B的坐标为$(-6, 3)$,横坐标为负,纵坐标为正,位于第二象限,不符合要求。
选项C的坐标为$(3, -4)$,横坐标为正,纵坐标为负,位于第四象限,符合要求。
选项D的坐标为$(5, 2)$,横坐标为正,纵坐标为正,位于第一象限,不符合要求。
因此,小手盖住的点的坐标可能为$(3, -4)$。
3. 地球的平均半径大约为$6.4× 10^{3}\ km$,这个近似值精确到(
A.个位
B.十分位
C.十位
D.百位
D
)A.个位
B.十分位
C.十位
D.百位
答案:D
解析:
首先,将$6.4 × 10^{3}$展开为普通数,即$6400$。
观察这个数,可以看到$6.4$中的$0.4$部分在乘以$10^{3}$后,变成了$400$,即精确到了百位。
因为$6.4 × 10^{3}$中的$6.4$表示的是$64$个百,所以近似值精确到百位。
观察这个数,可以看到$6.4$中的$0.4$部分在乘以$10^{3}$后,变成了$400$,即精确到了百位。
因为$6.4 × 10^{3}$中的$6.4$表示的是$64$个百,所以近似值精确到百位。
4. 在实数$\frac{1}{2},-3.14,\pi,|-2|,\sqrt{4},\sqrt{7},\sqrt[3]{9},0.808008…$中,无理数有(
A.2个
B.3个
C.4个
D.5个
C
)A.2个
B.3个
C.4个
D.5个
答案:C
解析:
无理数是不能表示为两个整数之比的数,常见的无理数包括:
1. 无限不循环小数,如$\pi$;
2. 某些开方开不尽的数,如$\sqrt{7}$;
3. 某些看似有规律但实际不循环的小数,如$0.808008…$。
现在,逐一判断给出的数是否为无理数:
$\frac{1}{2}$:这是一个有理数,因为它可以表示为两个整数之比。
$-3.14$:这是一个有限小数,因此它是有理数。
$\pi$:这是一个无理数,因为它是无限不循环小数。
$|-2|$:这是2,是一个整数,因此它是有理数。
$\sqrt{4}$:这是2,是一个整数,因此它是有理数。
$\sqrt{7}$:这是一个无理数,因为7的平方根不能表示为两个整数之比,且是无限不循环小数。
$\sqrt[3]{9}$:这也是一个无理数,因为9的立方根不能表示为两个整数之比,且是无限不循环小数(虽然不能直接开出,但根据无理数的定义,它仍然是无理数)。
$0.808008…$:这是一个无限不循环小数,因此它是无理数。
综上所述,无理数有:$\pi$,$\sqrt{7}$,$\sqrt[3]{9}$,$0.808008…$,共4个。
1. 无限不循环小数,如$\pi$;
2. 某些开方开不尽的数,如$\sqrt{7}$;
3. 某些看似有规律但实际不循环的小数,如$0.808008…$。
现在,逐一判断给出的数是否为无理数:
$\frac{1}{2}$:这是一个有理数,因为它可以表示为两个整数之比。
$-3.14$:这是一个有限小数,因此它是有理数。
$\pi$:这是一个无理数,因为它是无限不循环小数。
$|-2|$:这是2,是一个整数,因此它是有理数。
$\sqrt{4}$:这是2,是一个整数,因此它是有理数。
$\sqrt{7}$:这是一个无理数,因为7的平方根不能表示为两个整数之比,且是无限不循环小数。
$\sqrt[3]{9}$:这也是一个无理数,因为9的立方根不能表示为两个整数之比,且是无限不循环小数(虽然不能直接开出,但根据无理数的定义,它仍然是无理数)。
$0.808008…$:这是一个无限不循环小数,因此它是无理数。
综上所述,无理数有:$\pi$,$\sqrt{7}$,$\sqrt[3]{9}$,$0.808008…$,共4个。
5. 下列函数中,正比例函数是(
A.$y= \frac{2}{5x}$
B.$y= \frac{2}{5}x-1$
C.$y= \frac{4}{5}x^{2}$
D.$y= -\frac{2}{5}x$
D
)A.$y= \frac{2}{5x}$
B.$y= \frac{2}{5}x-1$
C.$y= \frac{4}{5}x^{2}$
D.$y= -\frac{2}{5}x$
答案:D
解析:
正比例函数的一般形式为 $y = kx$($k$ 是常数,$k\neq0$,$x$ 的次数为$1$)。
选项A:$y = \frac{2}{5x}$,可变形为$y=\frac{2}{5}\cdot\frac{1}{x}$,自变量$x$在分母位置,是反比例函数,不是正比例函数。
选项B:$y = \frac{2}{5}x - 1$,是一次函数,因为存在常数项$-1$,不符合正比例函数$y = kx$的形式,不是正比例函数。
选项C:$y = \frac{4}{5}x^{2}$,自变量$x$的次数是$2$,是二次函数,不是正比例函数。
选项D:$y = -\frac{2}{5}x$,符合正比例函数$y = kx$($k=-\frac{2}{5}\neq0$)的形式,是正比例函数。
选项A:$y = \frac{2}{5x}$,可变形为$y=\frac{2}{5}\cdot\frac{1}{x}$,自变量$x$在分母位置,是反比例函数,不是正比例函数。
选项B:$y = \frac{2}{5}x - 1$,是一次函数,因为存在常数项$-1$,不符合正比例函数$y = kx$的形式,不是正比例函数。
选项C:$y = \frac{4}{5}x^{2}$,自变量$x$的次数是$2$,是二次函数,不是正比例函数。
选项D:$y = -\frac{2}{5}x$,符合正比例函数$y = kx$($k=-\frac{2}{5}\neq0$)的形式,是正比例函数。
6. 关于函数$y= -2x+1$,下列结论中,正确的是(
A.图象必经过点$(-2,1)$
B.y随x的增大而增大
C.图象经过第一、二、三象限
D.当$x>\frac{1}{2}$时,$y<0$
D
)A.图象必经过点$(-2,1)$
B.y随x的增大而增大
C.图象经过第一、二、三象限
D.当$x>\frac{1}{2}$时,$y<0$
答案:D
解析:
A. 对于函数$y = -2x + 1$,当$x = -2$时,$y = -2×(-2) + 1 = 5$,所以图象不经过点$(-2,1)$,故A选项错误;
B. 由于函数的斜率$k = -2 < 0$,根据一次函数的性质,当$k < 0$时,$y$随$x$的增大而减小,故B选项错误;
C. 函数的斜率$k = -2 < 0$,且截距$b = 1 > 0$,根据一次函数图象与系数的关系,图象只能经过第一、二、四象限,不能经过第三象限,故C选项错误;
D. 对于函数$y = -2x + 1$,当$y = 0$时,$x = \frac{1}{2}$。由于$k < 0$,所以当$x > \frac{1}{2}$时,$y < 0$,故D选项正确。
B. 由于函数的斜率$k = -2 < 0$,根据一次函数的性质,当$k < 0$时,$y$随$x$的增大而减小,故B选项错误;
C. 函数的斜率$k = -2 < 0$,且截距$b = 1 > 0$,根据一次函数图象与系数的关系,图象只能经过第一、二、四象限,不能经过第三象限,故C选项错误;
D. 对于函数$y = -2x + 1$,当$y = 0$时,$x = \frac{1}{2}$。由于$k < 0$,所以当$x > \frac{1}{2}$时,$y < 0$,故D选项正确。
7. 若等腰三角形的两边长分别是3和6,则这个三角形的周长是(
A.12
B.15
C.12或15
D.9
B
)A.12
B.15
C.12或15
D.9
答案:B
解析:
1. 根据等腰三角形的性质,等腰三角形的两腰相等。
2. 题目给出等腰三角形的两边长分别是3和6,需要判断哪一边是腰。
3. 假设腰长为3,则三角形的三边分别为3、3、6。根据三角形的三边关系,任意两边之和应大于第三边,但3+3=6,不满足三角形的三边关系。
4. 假设腰长为6,则三角形的三边分别为6、6、3。此时满足三角形的三边关系,因为6+6>3,6+3>6,3+6>6。
5. 因此,等腰三角形的腰长应为6,底边长为3。
6. 三角形的周长为6+6+3=15。
2. 题目给出等腰三角形的两边长分别是3和6,需要判断哪一边是腰。
3. 假设腰长为3,则三角形的三边分别为3、3、6。根据三角形的三边关系,任意两边之和应大于第三边,但3+3=6,不满足三角形的三边关系。
4. 假设腰长为6,则三角形的三边分别为6、6、3。此时满足三角形的三边关系,因为6+6>3,6+3>6,3+6>6。
5. 因此,等腰三角形的腰长应为6,底边长为3。
6. 三角形的周长为6+6+3=15。
8. 已知点$(a,y_{1}),(a+1,y_{2})在一次函数y= -\frac{1}{2}x+2$的图象上,则$y_{1}与y_{2}$的大小关系是(
A.$y_{1}>y_{2}$
B.$y_{1}= y_{2}$
C.$y_{1}<y_{2}$
D.不能确定
A
)A.$y_{1}>y_{2}$
B.$y_{1}= y_{2}$
C.$y_{1}<y_{2}$
D.不能确定
答案:A
解析:
已知一次函数 $ y = -\frac{1}{2}x + 2 $,其斜率 $ k = -\frac{1}{2} < 0 $,说明函数单调递减。
点 $(a, y_1)$ 和 $(a+1, y_2)$ 在该函数图象上,故:
$ y_1 = -\frac{1}{2}a + 2 $,
$ y_2 = -\frac{1}{2}(a+1) + 2 = -\frac{1}{2}a - \frac{1}{2} + 2 = -\frac{1}{2}a + \frac{3}{2} $。
比较 $ y_1 $ 和 $ y_2 $:
$ y_1 - y_2 = \left(-\frac{1}{2}a + 2\right) - \left(-\frac{1}{2}a + \frac{3}{2}\right) = 2 - \frac{3}{2} = \frac{1}{2} > 0 $,
因此 $ y_1 > y_2 $。