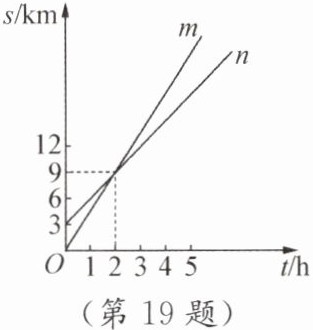
19. A,B两人相距3 km,他们同时朝同一目的地匀速直行,并同时到达目的地,行驶过程中两人的路程s km与时间t h的函数关系的图象如图所示.已知A的速度比B快,请根据图象判断:
(1) 图中的图象
(2) B的速度是
(1) 图中的图象
m
表示A的运动;(2) B的速度是
3
km/h.
答案:(1) $m$;(2) $3$
解析:
(1)由图可知,$m$在$2$小时走了$12$千米,$n$在超过$2$小时走了$12$千米,因为$A$的速度比$B$快,所以图中的图象$m$表示$A$的运动。
(2)由图可知,$B$在$2$小时走了$6$千米,根据速度公式$v = s÷ t$,其中$s = 6$千米,$t = 2$小时,可得$B$的速度$v=6÷2 = 3$(千米/小时)。
(2)由图可知,$B$在$2$小时走了$6$千米,根据速度公式$v = s÷ t$,其中$s = 6$千米,$t = 2$小时,可得$B$的速度$v=6÷2 = 3$(千米/小时)。
20. 已知一次函数$y= kx+b$,当$1\leq x\leq 4$时,$3\leq y\leq 6$,则$\frac{b}{k}$的值是
2或-7
.答案:$2$或$-7$
解析:
当$k > 0$时,函数为增函数。
当$x = 1$时,$y$取最小值$3$;当$x = 4$时,$y$取最大值$6$。
代入得:
$\begin{cases}k + b = 3 \\4k + b = 6\end{cases}$
解得:
$\begin{cases}k = 1 \\b = 2\end{cases}$
此时,$\frac{b}{k} = 2$。
当$k < 0$时,函数为减函数。
当$x = 1$时,$y$取最大值$6$;当$x = 4$时,$y$取最小值$3$。
代入得:
$\begin{cases}k + b = 6 \\4k + b = 3\end{cases}$
解得:
$\begin{cases}k = -1 \\b = 7\end{cases}$
此时,$\frac{b}{k} = -7$。
综上,$\frac{b}{k}$的值为$2$或$-7$。
当$x = 1$时,$y$取最小值$3$;当$x = 4$时,$y$取最大值$6$。
代入得:
$\begin{cases}k + b = 3 \\4k + b = 6\end{cases}$
解得:
$\begin{cases}k = 1 \\b = 2\end{cases}$
此时,$\frac{b}{k} = 2$。
当$k < 0$时,函数为减函数。
当$x = 1$时,$y$取最大值$6$;当$x = 4$时,$y$取最小值$3$。
代入得:
$\begin{cases}k + b = 6 \\4k + b = 3\end{cases}$
解得:
$\begin{cases}k = -1 \\b = 7\end{cases}$
此时,$\frac{b}{k} = -7$。
综上,$\frac{b}{k}$的值为$2$或$-7$。
21. (12分)(1) 计算:$\sqrt[3]{-8}+\sqrt{2}+\sqrt{(-2)^{2}}$;
(2) 已知$(x-1)^{2}= 9$,求x的值.
(2) 已知$(x-1)^{2}= 9$,求x的值.
答案:(1)
解:
首先计算立方根部分:
$\sqrt[3]{-8} = -2$
接着计算平方根部分:
$\sqrt{2}$ 保持不变,因为它已经是最简形式。
再计算平方后再开方的部分:
$\sqrt{(-2)^{2}} = \sqrt{4} = 2$
将上述三部分相加得:
$-2 + \sqrt{2} + 2 = \sqrt{2}$
(2)
解:
已知 $(x-1)^{2} = 9$
开方得:
$x - 1 = \pm 3$
分别解两个一元一次方程:
当 $x - 1 = 3$ 时,解得 $x = 4$
当 $x - 1 = -3$ 时,解得 $x = -2$
解:
首先计算立方根部分:
$\sqrt[3]{-8} = -2$
接着计算平方根部分:
$\sqrt{2}$ 保持不变,因为它已经是最简形式。
再计算平方后再开方的部分:
$\sqrt{(-2)^{2}} = \sqrt{4} = 2$
将上述三部分相加得:
$-2 + \sqrt{2} + 2 = \sqrt{2}$
(2)
解:
已知 $(x-1)^{2} = 9$
开方得:
$x - 1 = \pm 3$
分别解两个一元一次方程:
当 $x - 1 = 3$ 时,解得 $x = 4$
当 $x - 1 = -3$ 时,解得 $x = -2$
22. (12分)已知一次函数$y= kx-3的图象经过点(1,-2)$.
(1) 求这个一次函数的表达式.
(2) 点$(2,-1)$是否在此函数的图象上?说明理由.
(3) 当x为何值时,$y\leq 0$?
(1) 求这个一次函数的表达式.
(2) 点$(2,-1)$是否在此函数的图象上?说明理由.
(3) 当x为何值时,$y\leq 0$?
答案:(1) 将点 $(1, -2)$ 代入 $y = kx - 3$,得:
$-2 = k \cdot 1 - 3$
解得 $k = 1$,故一次函数表达式为 $y = x - 3$。
(2) 当 $x = 2$ 时,代入 $y = x - 3$,得 $y = 2 - 3 = -1$。
点 $(2, -1)$ 的纵坐标与计算结果一致,故该点在此函数图象上。
(3) 解不等式 $x - 3 \leq 0$,得 $x \leq 3$。
即当 $x \leq 3$ 时,$y \leq 0$。
$-2 = k \cdot 1 - 3$
解得 $k = 1$,故一次函数表达式为 $y = x - 3$。
(2) 当 $x = 2$ 时,代入 $y = x - 3$,得 $y = 2 - 3 = -1$。
点 $(2, -1)$ 的纵坐标与计算结果一致,故该点在此函数图象上。
(3) 解不等式 $x - 3 \leq 0$,得 $x \leq 3$。
即当 $x \leq 3$ 时,$y \leq 0$。